Volume 14, Issue 6 (November & December 2023)
BCN 2023, 14(6): 787-804 |
Back to browse issues page
Download citation:
BibTeX | RIS | EndNote | Medlars | ProCite | Reference Manager | RefWorks
Send citation to:



BibTeX | RIS | EndNote | Medlars | ProCite | Reference Manager | RefWorks
Send citation to:
Azarmi F, Shalbaf A, Ashtiani S N M, Behnam H, Daliri M R. Early MS Identification Using Non-linear Functional Connectivity and Graph-theoretic Measures of Cognitive Task-fMRI Data. BCN 2023; 14 (6) :787-804
URL: http://bcn.iums.ac.ir/article-1-2276-en.html
URL: http://bcn.iums.ac.ir/article-1-2276-en.html
Farzad Azarmi1 

 , Ahmad Shalbaf *1
, Ahmad Shalbaf *1 

 , Seyedeh Naghmeh Miri Ashtiani2
, Seyedeh Naghmeh Miri Ashtiani2 

 , Hamid Behnam2
, Hamid Behnam2 

 , Mohammad Reza Daliri2
, Mohammad Reza Daliri2 




 , Ahmad Shalbaf *1
, Ahmad Shalbaf *1 

 , Seyedeh Naghmeh Miri Ashtiani2
, Seyedeh Naghmeh Miri Ashtiani2 

 , Hamid Behnam2
, Hamid Behnam2 

 , Mohammad Reza Daliri2
, Mohammad Reza Daliri2 


1- Department of Biomedical Engineering and Medical Physics, School of Medicine, Shahid Beheshti University of Medical Sciences, Tehran, Iran.
2- Department of Biomedical Engineering, School of Electrical Engineering, Iran University of Science & Technology, Tehran, Iran.
2- Department of Biomedical Engineering, School of Electrical Engineering, Iran University of Science & Technology, Tehran, Iran.
Keywords: Cognitive task-fMRI, Computational neuroscience, Kernel mutual information, Non-linear connectivity, Network measures, Machine learning system
Full-Text [PDF 2077 kb]
| Abstract (HTML)
Full-Text:
1. Introduction
Multiple sclerosis (MS) is an unforeseeable sickness that disrupts the function of the central nervous system (CNS) with an inflaming mechanism. MS obstructs the flow of information within the brain and between the brain and body. It is thought that MS is the most prevalent autoimmune disease among young adults affecting the CNS, which is characterized by the development of lesions in vital nerves (Lucchinetti et al., 2000; Mitolo, 2015; Nelson et al., 2017). MS patients may experience several types of symptoms, including motor, cognitive, and neuropsychiatric disorders. In this regard, a significant number of MS patients suffer from cognitive impairment (Ruano et al., 2017). Patients experience such deficits from the beginning of the disease, which leads to permanent disability. Cognitive impairment usually involves several functions of the brain (Ruano et al., 2017) that strongly affect several aspects of patients’ personal lives, and may finally, cause the reduction of life’s overall quality. Hence, early identification of the inflammatory mechanism allows patients to start therapy with an immunomodulatory agent well before receiving a clinical diagnosis of definitive MS, thus slowing the degenerative advancement of MS (Miller, 2004).
Tissue damage is prevalent among MS patients. If the compensatory brain processes cannot counter tissue damage, MS may enter the irreversible disability phase. Accordingly, functional magnetic resonance imaging (fMRI), as a promising modality, reveals the brain’s functional network reorganization when the compensatory processes are still efficient at the initial phases of the disease. Therefore, fMRI can be utilized for diagnosis in the initial phases of the disease. In this regard, blood oxygen level-dependent (BOLD) can record the data (Faivre et al., 2016). Specific tasks may be practical for the activating cognitive functions of the brain in fMRI sessions, among which the paced auditory serial addition test (PASAT) is prominent for the case of MS disease. Multiple cognitive domains are measured using PASAT (Sandry et al., 2016). As a result, the gray matter atrophy in MS is related to functional connectivity reorganization during the PASAT implementation (Baltruschat et al., 2015).
The performance of the human brain in a particular task is associated with the brain network. In recent studies, analysis of the brain networks through connectivity is of great concern. Brain connectivity analysis is an eminent concept for obtaining information from the cerebral network’s neural organization and assessing the brain’s performance. One well-known non-linear functional connectivity method is mutual information (MI), which led to reliable results in previous studies (Cassidy et al., 2014; Dimitriadis et al., 2018; Thompson & Fransson, 2015). According to the non-linear nature of the BOLD time series (Heinzle et al., 2016; Logothetis et al., 2001), MI is more likely to provide reliable results rather than linear connectivity measures. In addition, MI offers invaluable information about the linear properties of the data as well (Cohen, 2014). Several studies have analyzed fMRI or EEG data using MI to investigate the brain. For instance, Dimitriadis et al., (2018) used symbolic MI and showed that impaired children demonstrate a less effective network compared with healthy subjects in terms of cross-frequency interactions between brain regions. Gong et al. (Gong et al., 2018) used MI to study the physiologic pattern of motor imagery in four tasks. Cassidy et al. (Cassidy et al., 2014) used partial coherence obtained by sparse vector autoregressive (VAR) models to calculate the MI. However, MI has a potential drawback in that it is sensitive to the number of selected bins (Cohen, 2014). Moreover, MI is based on histograms, which are discontinuous, and may provide erroneous results due to the continuous nature of neural time series. Kernel MI (KMI) is a consistent method that does not have the drawbacks of MI. This method is insensitive to the choice of the origin, and more complicated window shapes may be conducted. Furthermore, it provides an enhanced mean square error in converging the estimation of the data. Therefore, KMI outperforms MI in terms of neural data analysis (Moon et al., 1995). In this regard, Wang et al. (2015). demonstrated that MI estimation using kernel functions is consistent with the symptoms of Alzheimer’s disease (AD).
One of the most intricate networks discovered is the human brain. In this regard, roughly 86 billion neurons allow the transmission of electrical and chemical signals in the brain. It is widely assumed that the graph theory development establishes a fundamental framework for gaining a deep comprehension of the brain, and provides exquisite insights into the biological process of the human brain in cognition (Farahani et al., 2019). There have been few studies on the brain network of MS patients. For example, graph theory was implemented via resting-state fMRI to assess alteration in the brain networks among relapsing-remitting MS (RRMS) patients and healthy controls and the results demonstrated that the efficiency decreased in RRMS individuals. Also, the mean connectivity strength identified RRMS subjects and clinically isolated syndrome (CIS) individuals from healthy subjects with a 77% accuracy in each category (Liu et al., 2017). Ashtiani et al., (2018) also used graph theory for assessing MS disease. They reported several informative regions between healthy and MS subjects. They also discovered that small worldness and clustering coefficient were greater in healthy controls (HCs) compared to RRMS patients. Welton et al. (2020) used multiple cognitive tasks to test the reliability of network measures in predicting cognitive performance. They showed that damaged network structures can predict cognitive impairment in MS and that monitoring is accurate for one month.
The present study aimed to evaluate the alteration in brain network based on a non-linear connectivity measure using cognitive task-fMRI data between MS patients at initial phases and HCs. In this regard, discriminative graph measures and informative regions must be specified using a prominent statistical test. Moreover, the particular features for data classification must be chosen. Hence, a robust method for feature selection and classification must be proposed. According to the literature, no research used KMI via task data to present cognitive impairment in MS patients using graph measures. Hence, we conducted KMI in this study and constructed a graph network using the results of connectivity analysis using BOLD fMRI data, and used PASAT in the experimentation to activate cognitive functions of the brain. The brain time series was extracted from each region using automated anatomical labeling (AAL) atlas. Afterward, network measures in each subject were extracted. The best size of the kernel window was found using searching over a wide range of kernel widths according to the best result of the classification section. Then, a between-class significance test was implemented on the data between patients and HCs. The classification was employed on the results using different hyperparameters of the decision tree and support vector machine (SVM). The results obtained in the present study were compared with the previous study with the same data (Ashtiani et al., 2018) using classification performance metrics.
2. Materials and Methods
Dataset description
Twenty subjects participated in the present study, including eight patients (seven women and one man) in the initial phases, and 12 HCs (eight women and four men). All participants were right-handed, determined by McDonald’s criteria (Polman et al., 2005). The patients suffered from RRMS. All patients were between 26 and 44 years old. Patients were diagnosed an average of 30 months before the trial (ranging from 8 to 60 months). HCs were between 23 to 40 years old with a mean age of 30.67. The expanded disability status scale (EDSS) score was below 3.5 for patients. This means patients had a minimal physical disability and were in the initial phases. It is essential to note that patients with <5 years of diagnosis of the disease were chosen for this study. Furthermore, the participants filled out a consent form before the experiment. The patients were not in the attack phase during the experimental procedure, and at least three weeks had passed since the last hospitalization for the experiment.
Experimental paradigm
PASAT was used to test memory, executive functioning, and information processing as cognitive functions. The modified version of the PASAT was used in this study. In the original version, a digit between 0 and 9 is played every 3 seconds using an audio headset, and the participant has to press a response box key if the summation of two sequential numbers is below ten, while they have to prevent doing such action, otherwise. The summation number was altered to 11 in this experiment, and the language of the test was Persian. We used the block design to conduct the experiment by implementing the active and rest stages. The duration of each stage was 30 seconds. In the active stage, the participants had to perform the PASAT procedure. However, they had to close their eyes in the resting stage and try to think about nothing. The total duration of the experiment was 6 minutes, including six times at each stage. As a result, 12 phases were employed in the experimentation of each subject.
In this experiment, a 3 Tesla Siemens Tim Trio system was employed to obtain structural and functional MRI images. Echo planar imaging (EPI) was used for functional images (repetition time 2 s, echo time=30 ms, field of view=192 mm2, and flip angle=90°) and the structural images were constructed by means of a high-resolution T1-weighted MPRAGE pulse sequence (repetition time=1.8 s, echo time=3.44 ms, flip angle=7° ). A detailed description of the experimental paradigm can be found in a previous study (Ashtiani et al., 2018).
Data analysis pipeline
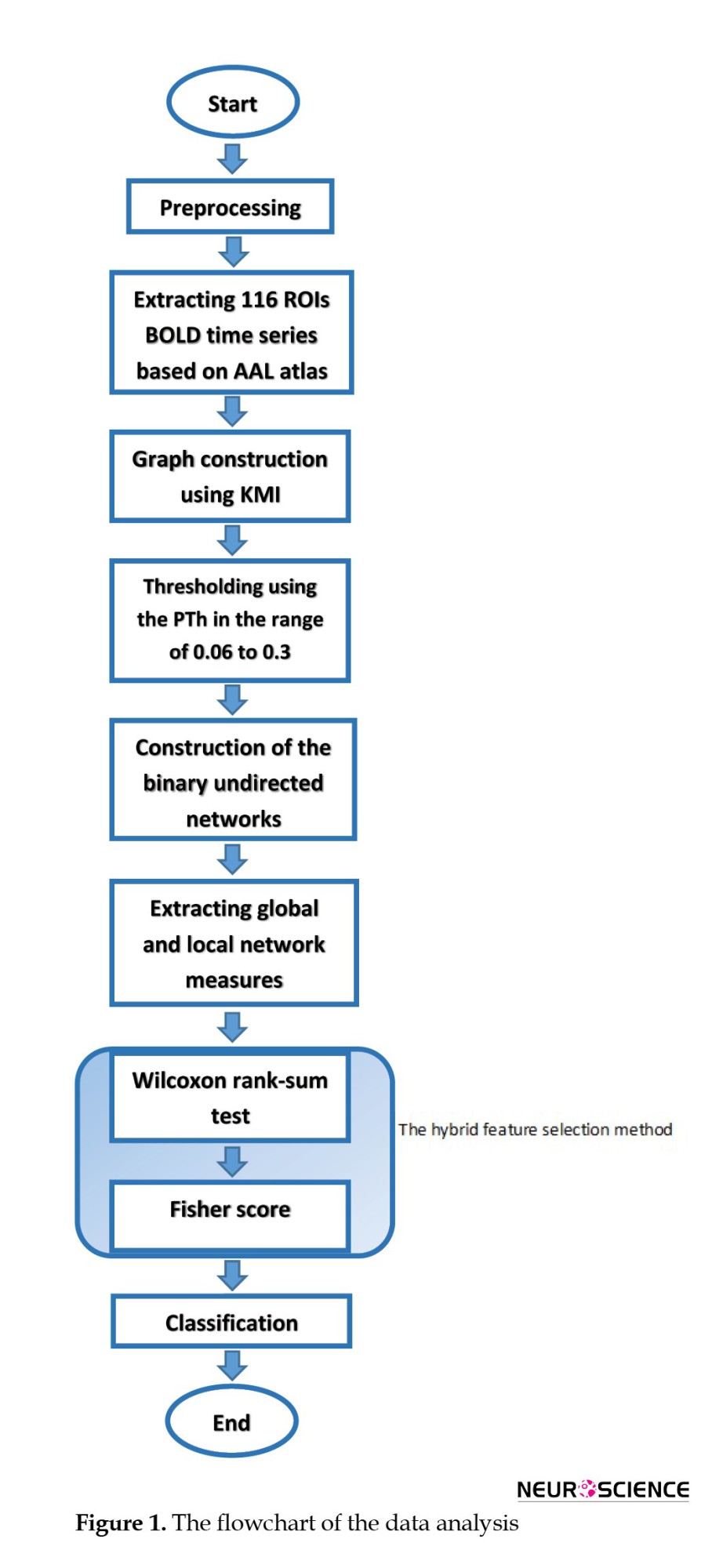
The procedure of data analysis is illustrated in Figure 1. A hybrid feature selection method was implemented in the present study using the Wilcoxon rank-sum test with the Fisher score. The same procedure has been repeated using the correlation and MI-based network to compare the classification results of the correlation and MI-based networks and KMI-based networks.
Preprocessing
FEAT fMRI analysis was used to conduct preprocessing on FSL (FMRIB’s Software Library). The preprocessing pipeline is demonstrated in Figure 2. MCFLIRT, BET, and FLIRT (Jenkinson et al., 2002; Jenkinson & Smith, 2001; Smith, 2002) options were used to implement the preprocessing stage. The detailed steps of preprocessing are described in a previous study (Ashtiani et al., 2018).

Brain network construction via kernel estimation of MI
Neuroimaging studies often require dividing the brain into parcels (regions) with homogenous properties The AAL atlas was utilized in order to parcellate the brain into 116 regions of interest (ROIs). The averaging method was implemented to obtain the signal of each parcel. The brain connectivity of each pair of parcels was determined after the signals of regions were extracted. Having two signals, X and Y, the MI between X and Y is defined as Equation 1:
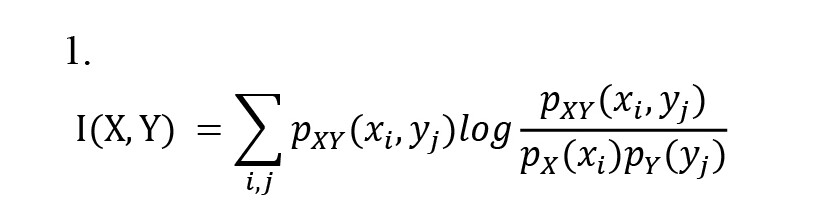
Where, px(x) is the marginal probability of X and py(y) is the marginal probability Y. Also pxy(x, y) is the joint probability of X and Y. The probability values in the above statement are estimated by binning the distributions and creating a histogram (Cover & Thomas, 2012). KMI, however, applies the Gaussian kernel function rather than binning the distribution (Beirlant et al., 1997). The Equations 2, 3, 4 statements show the probabilities employed using Gaussian kernel functions:

Here, h is a parameter for controlling the width of the kernel, which is defined based on σ, the standard deviation of the kernel. KMI can be used as a functional connectivity method, in which interdependence between regions is extracted. KMI can be defined as Equation 5:

We used each brain’s whole time series as X and Y and constructed connectivity matrices for all of the subjects using KMI in the whole 12 phases of active and rest. Therefore, the brain network of each subject will be constructed. Assuming σ as the standard deviation of the Gaussian kernel, various standard deviations, including 2, 1.5, 1, 0.5, 0.25, and 0.125, were used in this method. However, we considered σ equal to 0.25 for reporting the results since the best classification accuracy was achieved in such a condition. We considered each ROI as a node and measures of connectivity as edges of a graph for each subject and constructed the connectivity matrices. The KMI was employed using FastPairMI.m for extracting the connectivity matrices (Qiu et al., 2009).
Thresholding and extracting the graph measures
Thresholding, selecting the most consistent set of edges that jointly construct the graph, is a typical analysis stage in forming a functional graph. Each subject’s network is different from other numbers and weighs on the edges (Wen et al., 2011). Proportional thresholding (PTh) is a prominent matching strategy prior to statistical and machine learning implementations. In this approach, a specified number of the most robust connections are chosen as network edges to ensure equal network density across participants’ brain networks (Gamboa et al., 2014). The PTh method was used in this study in the range of 0.06 to 0.3 with steps equal to 0.01 to threshold the adjacency matrices. Then, each of the resulting matrices was transformed into binary. Afterward, we extracted brain graph measures from binary matrices. Using the BrainNet viewer, Figure 3 displays the full mesh graph and threshold network of a single subject at a PTh value equal to 0.19 (Xia et al., 2013).

Brain networks are commonly described using graph theory measures to show the properties of the brain structure. It is widely assumed that the brain’s substrate is a complex network. This concept is represented through several graph measures in this study. Accordingly, assortativity, characteristic path length, global efficiency, mean clustering coefficient, modularity, and transitivity were used as global measures. In addition, the betweenness centrality, degree, eigenvector centrality, k-coreness centrality, PageRank centrality, participation coefficient, and sub-graph centrality were employed as local measures.
Significance test, feature ranking, and classification
Comparing two groups is a prevalent type of scientific experimentation The Wilcoxon rank-sum test is a well-known nonparametric test for non-normal distributions, which was the case for the obtained graph measures. This test was applied to the extracted graph measures (P<0.05). The criterion for considering a measure as discriminating was that it was statistically significant at more than 12 threshold numbers (approximately half the range) in each global measure or measurement area for local measures.
Significant features were considered as the input of the feature ranking method. Multiple feature ranking methods were employed on graph measures, yet none was as robust as the Fisher score. Fisher score is a feature selection algorithm independent of class distribution that can specify the distinction power of each feature between the classes (Duda et al., 2012). The best combination of discriminative features was selected using the Fisher score by ranking the features. Afterward, we selected various combinations of the best features ranging from 1 to 10 to avoid overfitting regarding the sample size. These features were used for classification using different parameters of SVM and the decision tree. The optimal feature set is the combination, by which the highest accuracy could be obtained (Acharya et al., 2015; Ahmadi et al. 2020; Ahmadi et al., 2019). Fisher score was used within the leave-one-subject-out-cross validation (LOOCV) to avert interdependency. In other words, the Fisher score was implemented on the training set in each fold separately, and the selected features were then used on the test data in that fold. Standard performance metrics of classification, such as accuracy, sensitivity, specificity, as well as Cohen’s kappa coefficient were employed in this study. In this regard, Cohen’s kappa measures the agreement among two raters that classify N items into C mutually individual categories. This measure is strongly recommended when the labels are imbalanced. The rate of agreement categorization is previously discussed (McHugh, 2012).
3. Results
We obtained the graph features of the brain by constructing the networks via KMI. The statistical test was then used between the groups to obtain informative regions and discriminative features. Afterward, we used a combination of a statistical test and feature ranking as a hybrid feature selection method.
Hypothesis testing of global features
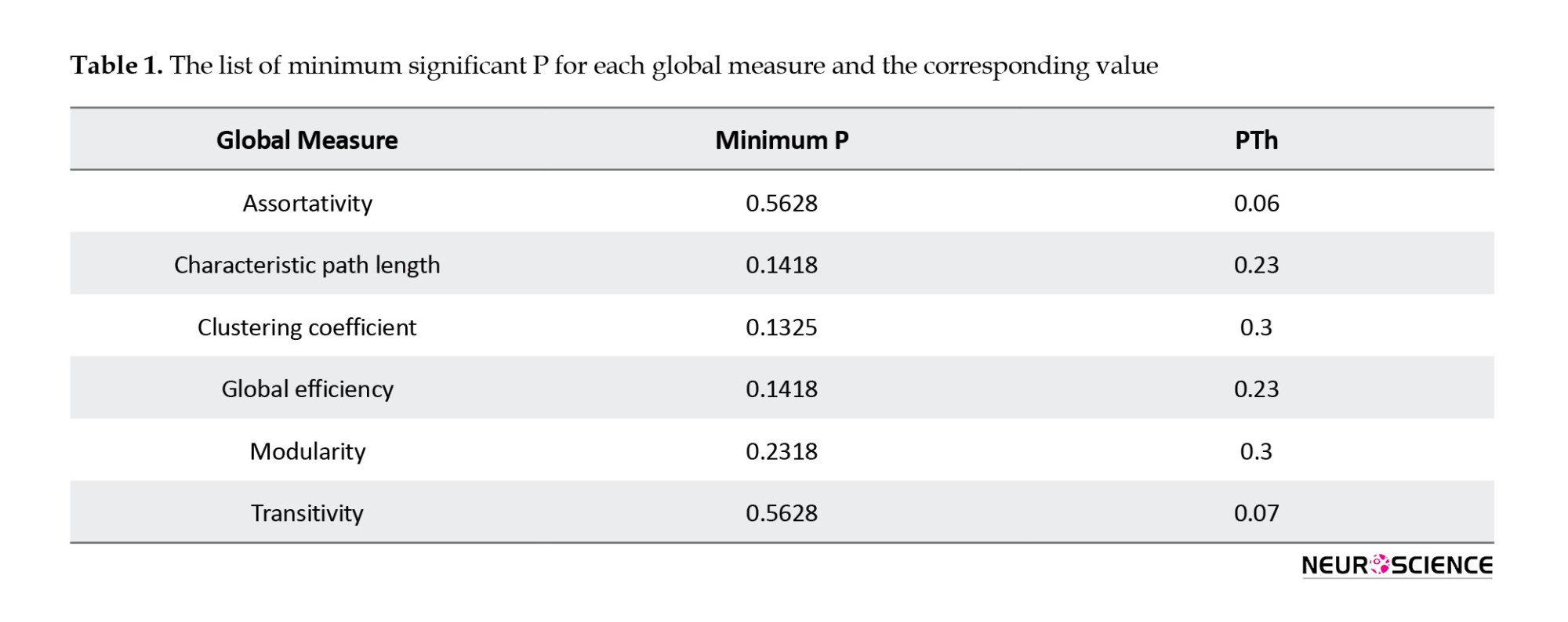
Altered global measures between the two groups can demonstrate changes in networks and the topology of the brain. In this study, significant values were not obtained in such measures. Table 1 demonstrates the lowest P in each measure and the corresponding PTh.
Hypothesis testing of local features
Damaged areas can alter brain topology and subsequently change local properties obtained from the mentioned areas. The degree, k-coreness centrality, betweenness centrality, participation coefficient, eigenvector centrality, PageRank centrality, and subgraph centrality were discriminative within several areas. Such measures and their corresponding informative regions are listed in Table 2.

The P and the corresponding threshold are reported for each region. Figure 4 also shows all discriminative regions.

Classification performance
Based on the Fisher score, we picked the best combination of features from 1-10 features for each classification method in order to avoid overtraining. The highest classification outcome investigated by the optimum parameters of each classifier via the graph measures of KMI-based networks is shown in Table 3.

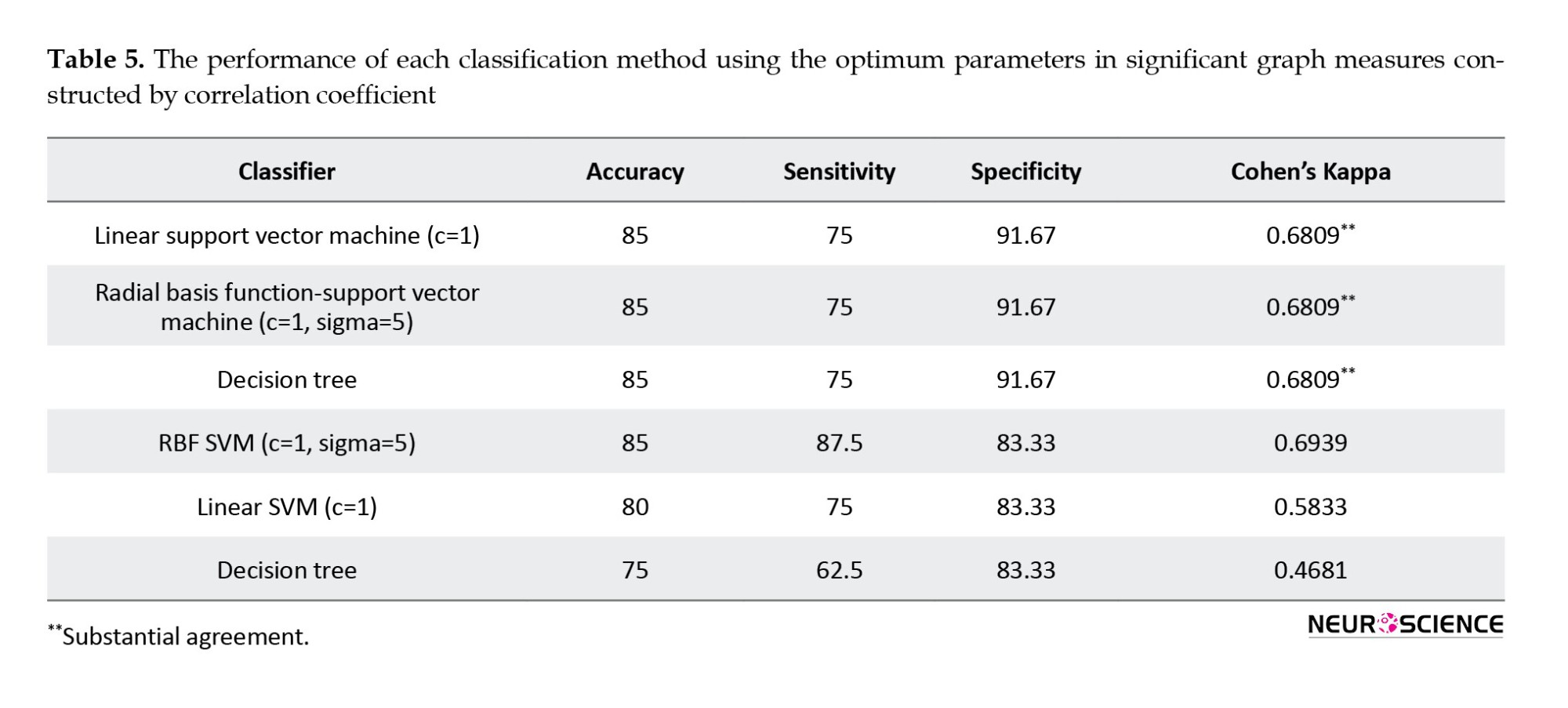
Radial basis function SVM (RBF-SVM) had the greatest accuracy (95%) (PTh=0.09). The accuracy of RBF-SVM (PTh=0.09) in different combinations of measures is shown in Figure 5. The corresponding procedures were implemented using correlation coefficient and MI for comparison, and the results are reported in Tables 4 and 5 respectively. The best classification accuracy using the correlation coefficient and MI-based method were 85% and 90%, respectively.
The most repeated measures selected using the Fisher score using correlation-based networks were left Fusiform in degree and PageRank centrality as well as left hippocampus and left parahippocampal in k-coreness centrality, yet the most repeated measures selected using the Fisher score in KMI-based networks were left Pallidum in degree, eigenvector centrality, k-coreness centrality, and PageRank centrality as well as left parahippocampal in eigenvector centrality, k-coreness centrality, and PageRank centrality.
The corresponding measures for MI were the right hippocampus in betweenness centrality and the left pallidum in eigenvector centrality.
Significance test on connectivity
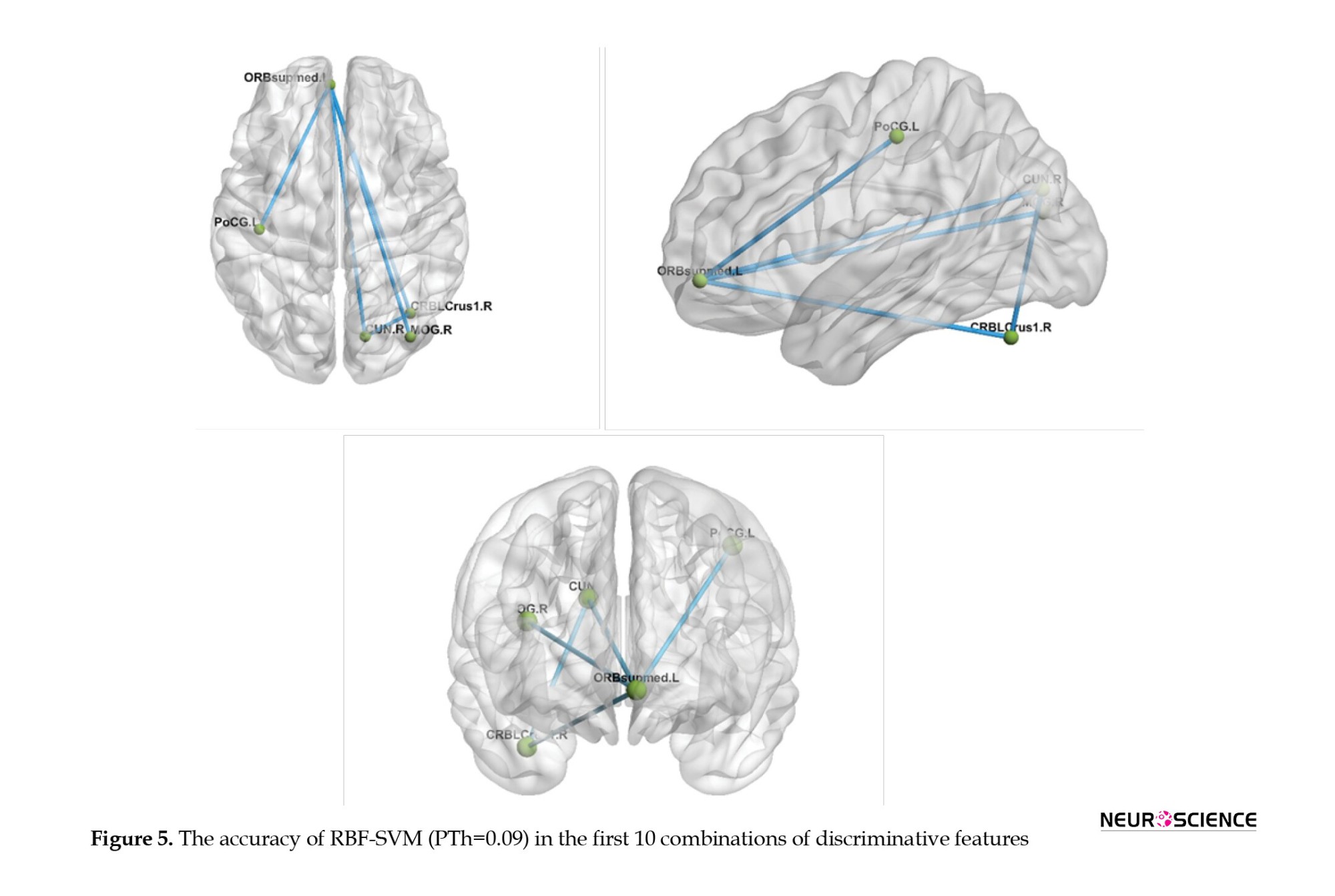
The significant difference in connectivity matrices was achieved using the Wilcoxon rank-sum test (P<0.05, FDR corrected). The number of significant connections was 3446 without FDR correction. However, this value decreased to five via FDR correction. The connectivity measure between the left medial orbitofrontal cortex and right cuneus, right middle occipital gyrus, left postcentral gyrus and, right crus I of the cerebellar hemisphere and right cuneus and right crus I of the cerebellar hemisphere were significantly different. Figure 6 also shows the significant connections in a brain sample.

Classification accuracy and feature selection of connectivity
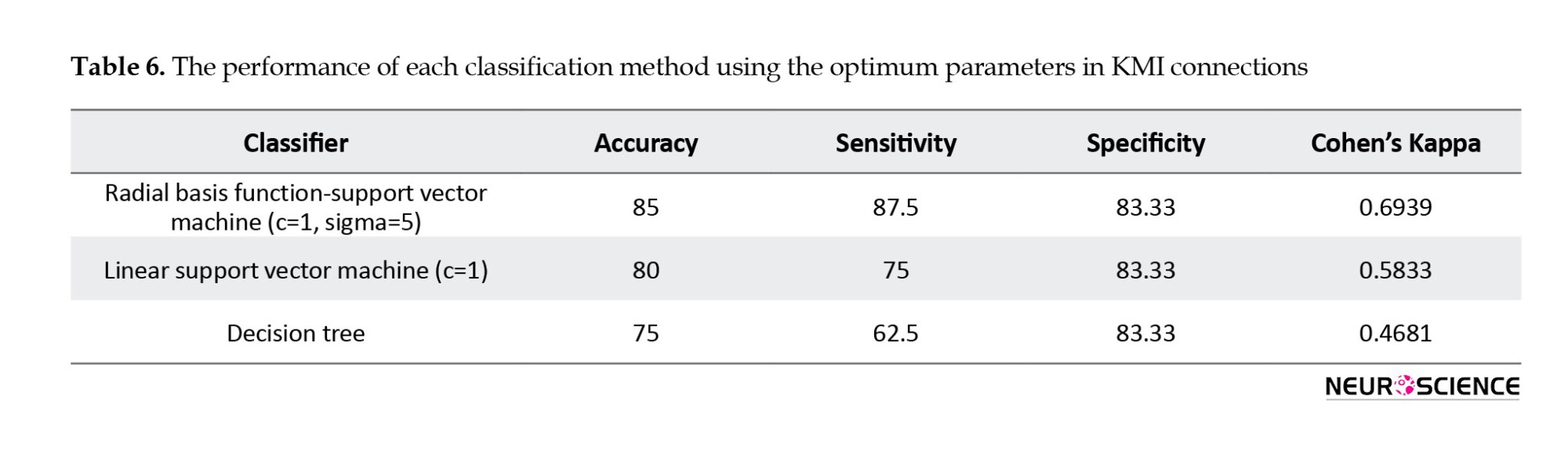
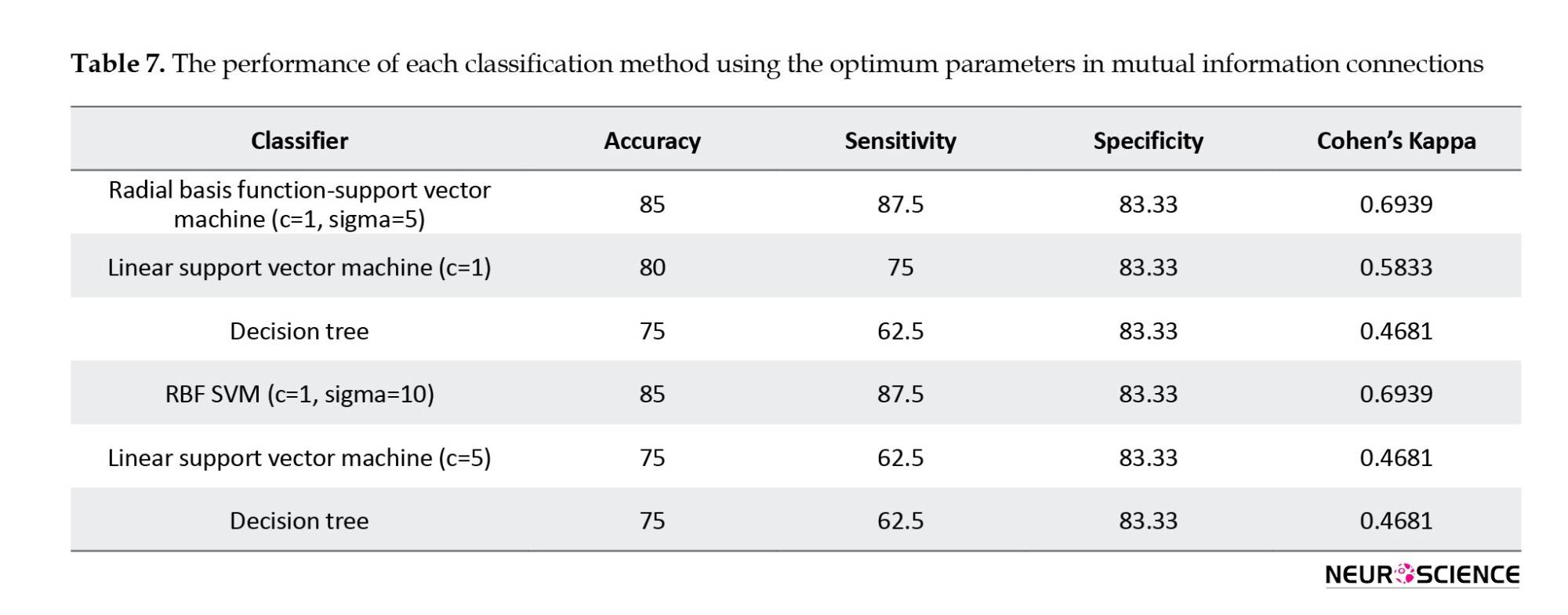
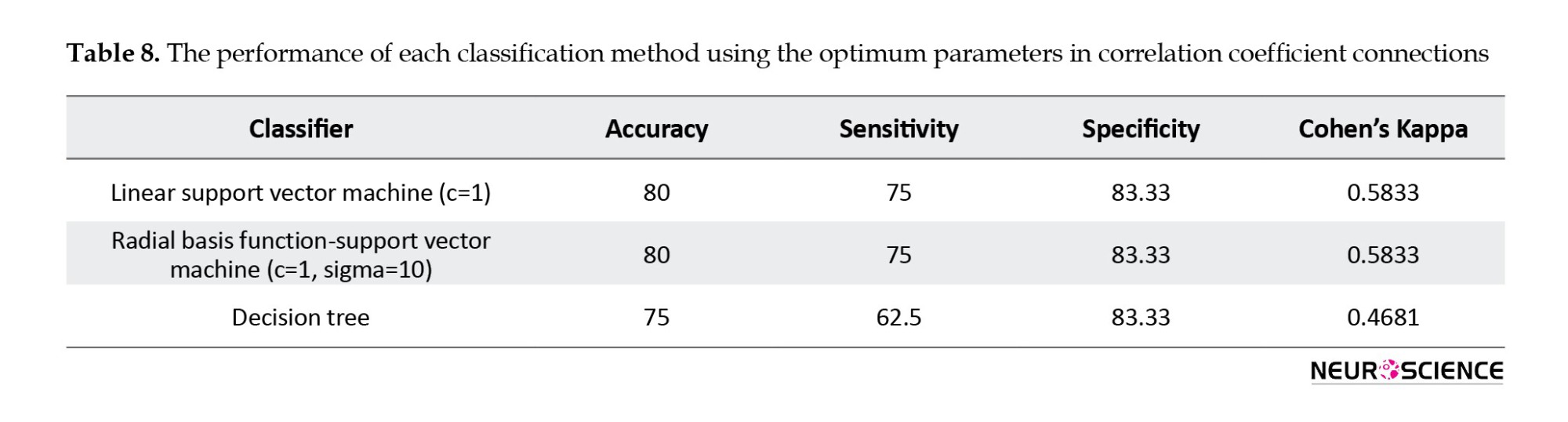
The method for classifying connectivity values is the same as the process for classifying network measures. The Wilcoxon rank-sum test was used to derive the discriminative connectivity values. Then, we used the Fisher score to classify the data by using LOOCV. Tables 6, 7, 8 show the best classification outcome for connectivity measures.
The findings suggest that in terms of classification, connectivity values are not as reliable as network measures. However, Liu et al., (2017) mentioned that functional connectivity is a more discriminatory method than traditional activity patterns in an fMRI study.
4. Discussion
The present study aimed to assess the brain graph’s alteration in the early phases of MS compared to a healthy brain, primarily to assess the cognitive effects of the disease. Hence, we used fMRI during the performance of PASAT to analyze the brain network of MS patients compared to HCs. The classification was implemented to test the validity of the discriminative graph measures.
It is widely assumed that the BOLD fMRI time series contains non-linear properties. Accordingly Lahaye et al. (2003) found that connectivity measures obtained from the BOLD fMRI time series are unlikely to contain only linear instantaneous information. As a result, a non-linear connectivity measure was employed in this study for constructing subjects’ brain networks. Non-linear connectivity measures have superior performance over linear measures (Deshpande et al., 2006; Karanikolas et al., 2016; Li et al., 2010). In addition, Zhao et al. (2020) demonstrated the excellent performance of non-linear connectivity analysis in an electroencephalogram (EEG) study. Yang et al. (2016) also proved that the incorporation of higher-order non-linearities offers a complete inference of the phase coupling. Using a kernel function, as a non-linear approach, has a promising result in the network analysis of AD by Ahmadi et al. (2020), and leads to a robust distinction between HCs and patients in fMRI analysis. Non-linear connectivity measures, like KMI, outperform linear measures using EEG data (Afshani et al., 2015).
Several centrality measures, including the degree, PageRank centrality, eigenvector centrality, subgraph centrality, and k-coreness centrality, were discriminative in almost the same regions. Central nodes are the most critical nodes of the graph in terms of interaction with other nodes, which can be demonstrated as the degree of a node in the simplest form. In other words, most centrality measures demonstrate the amount of node participation in short paths. Many studies have assessed the brain in terms of centrality measures in MS; for example, Eijlers et al., 2017 found that several regions showed altered degree and eigenvector centrality in cognitively impaired MS patients. The obtained regions were remarkably in line with our found regions. The PageRank centrality is similar to the eigenvector centrality, including a damping factor on contributing neighbors. Ashtiani et al., 2018 reported that the PageRank centrality altered in the hippocampus and segments of the cerebellum between the MS group and HCs. They also discovered that the sub-graph centrality, a graph measure that describes the contribution of every node in all subgraphs, was altered between MS patients and controls in the hippocampal, parahippocampal, postcentral, and cerebellar regions as well. The k-coreness centrality was assessed in AD several times previously, which resembles MS as to the cognitive effects of the disease. Khazaee et al. (2017) found that the k-coreness centrality is a relatively robust feature in identifying AD patients in resting-state fMRI. Sheng et al. (2019) also used the k-coreness for training a novel human connectome project multi-modal parcellation (HCPMMP) method in classifying MS patients from HCs. Ashtiani et al., (2018) also found that the k-coreness centrality is informative in MS.
In this study, merging the Wilcoxon rank-sum test with the Fisher score, as a hybrid approach, led to superior accuracy. According to our previous study (Azarmi et al., 2019) and the achieved results, it stands to reason that when the outputs of the Wilcoxon rank-sum test are used as the input of the Fisher score, greater accuracy may be obtained rather than using the Fisher score alone. The most particular features are elected using the Fisher score from the discriminative features via the mentioned approach. As a result, the obtained features are the most independent ones for classification.
The non-linearity of classification systems is an essential aspect of the present research. In non-linear classification, the boundary for separating categories is much more complex than in linear systems. Therefore, non-linear classification, as opposed to linear classification, is more flexible and less biased (Mørch et al., 1997). Accordingly, the RBF-SVM outperformed linear SVM based on our findings. In an fMRI study, Schmah et al. (2010) reported that non-linear classifiers, like RBF-SVM or second-degree polynomial SVM, outperformed linear SVM due to changes in brain connectivity. In another study, Yourganov et al. (2014) also reported that the results could be used for a wide range of connectivity deficit studies. MS is also a neurodegenerative disease that causes connectivity deficits in the brain’s connections. The decision tree was another classification method, which was used in this study. Zhao and Zhang, (2008) reported that decision trees are unstable, and a minor difference in the training data will lead to different attribute selections at each choice point in the tree. As a result, a significant impact may occur, since attribute choices influence all descendent subtrees. The decision tree performed better than linear SVM, yet it had a lower accuracy compared to RBF-SVM based on our results. It is worth noticing that the graph features picked using the proposed feature selection approach varied from those selected using correlation and MI with KMI-based networks.
The decision tree had a greater sensitivity compared to RBF-SVM. It is thought that identifying patients correctly is crucial in neuroscientific studies rather than HCs. In other words, detecting patients as HCs is a critical limitation in such studies. As a result, the decision tree might be a superior classification system compared to RBF-SVM from this perspective. The specificity of SVM in both kernels was 100%, which is consistent with our previous research (Azarmi et al., 2019).
According to Duda et al., (2012), when the data’s dimensionality is staggering, the Fisher score is one of the most prominent feature selection techniques. We implemented various methods of feature selection but finally, the Fisher score was selected. Thus, the accuracy of classification showed a prominent value. Khazaee et al. (2015) also used various feature selection methods and gained the best accuracy using fisher score in a resting-state fMRI study, which aligns with our results. It is worth mentioning that the present study aimed to determine the discriminative network measures and informative ROIs, which could classify HCs from MS patients. Moreover, dimensionality reduction methods convert the space of the features to another space. Hence, implementing the mentioned methods would not benefit us in gaining promising results.
Cohen’s kappa is a popular statistic for inter-rater and intra-rater checking in reliability (McHugh, 2012). According to the results, RBF-SVM and decision tree were in perfect agreement using the measures of KMI-based networks, and linear SVM was in substantial agreement. In addition, linear SVM was in perfect agreement using MI-based networks. However, all classification systems were in substantial agreement with the measures of correlation-based networks. The results showed that KMI outperforms the correlation coefficient as a measure of connectivity using a prominent classification metric.
The results obtained from KMI showed a more remarkable performance in accuracy, sensitivity, specificity, and Cohen’s kappa compared to the correlation coefficient. Accordingly, KMI can be considered a valid measure of connectivity over linear measures, like the correlation coefficient. Overall, the results are expected according to the non-linear properties of KMI as well as the BOLD time series. Additionally, KMI does not have the drawbacks of MI, which is choosing the origin in binning and discontinuity. Moreover, it is computationally less complex than mode-based effective methods. Therefore, KMI is preferred to the mentioned methods. However, it is thought that multiple studies should be implemented on brain data in order to gain valid results.
Parahippocampal and pallidum regions were among the regions that were selected multiple times using the Fisher score. These regions were obtained several times in graph measures obtained by KMI or correlation coefficient. The function of the parahippocampal region is memory encoding and retrieval. Therefore, it can be assumed that this region is related to cognitive functions. Pallidum was chosen only via the KMI method and is related to voluntary movement. The hippocampus and fusiform were repeated several times using the correlation coefficient. The former plays a crucial role in memory functions, while the latter is related to word and face recognition. Both of these regions’ tasks are related to cognitive function.
Twelve ROIs were identified as discriminative regions in various local graph measures, and each of these regions has a particular functionality. All mentioned regions were associated with the impacts of MS, which are described in detail in the following sections.
Regions 14 and 16 of the AAL atlas were discriminative solely in participation coefficient and betweenness centrality, respectively. In this regard, the triangular part of the right inferior frontal gyrus is related to the go/no go task, which is significantly different in our study. A powerful response, like pressing a button or preventing performing such an action must be banned in this task. Accordingly, the go/no go task is similar to PASAT. Hence, we believe that this region might be involved in causing MS disease. Mainero et al. (2004) also reported a significant difference in the activation of this area among MS individuals and HCs while performing a recall task using fMRI data. The orbital part of the inferior frontal gyrus is also reported to be involved in causing autism, which is a neurodevelopmental disorder as well. Charil et al. (2007) reported an alteration in the thickness of the inferior frontal gyrus in RRMS patients. Trapp et al. (2018) also reported that demyelination and neuronal loss would happen in this area during MS progress. Chen et al. (2018) reported a significant difference in seed-based functional connectivity between the MS group and HCs in this region.
The hippocampus in both hemispheres of the brain and the parahippocampal gyrus in the right hemisphere were significantly different in our study, consistent with many previous studies (Kern et al., 2015; Koenig et al., 2018; Rocca et al., 2018; Vacchi et al., 2017; van Geest et al., 2018). The hippocampus is a critical region in transferring information from short-term to long-term memory as well as the organization of new memories from past experiences. This region is one of the first segments of the brain, which is damaged in AD. This region has a leading role in epilepsy and schizophrenia. In addition, the parahippocampal gyrus has a central role in memory encoding and recovery. These functions are of much importance when cognitive impairment occurs. The superior temporal pole was also reported as a region related to MS in other studies. For example, Vacchi et al., (2017) demonstrated that this region is involved in relapse-onset MS as a factor for memory dysfunction in the N-back task during the fMRI experiment. In another study, Tommasin et al. (2018) stated that the right superior temporal gyrus and left cerebellum VI lobule have different connectivity values between new MS patients and progressed MS patients, which means that the region contributes to MS during the progress of the disease.
One of the significant symptoms of MS patients is in movement control. The paracentral lobule is a supplementary motor area (SMA) segment, which contributes to motor functions. Four hypothesized functions are defined for SMA: The control of postural stability during stance or walking, temporal sequences of action coordination, bimanual coordination, and the initiation of internally generated as opposed to stimulus-driven movement. This region was reported to be related to MS several times in previous studies of fMRI (Boutière et al., 2017; Cui et al., 2017; Nelson et al., 2017; Spiteri, et al., 2017). It also is assumed that pallidum contributes to voluntary human movement. This region also plays a crucial role in MS. Tacchino et al. (2018) showed a negative correlation between the index of success and pallidum in RRMS patients as a function of disease severity in motor imagery. Meijer et al. (2018) also found that the connectivity attained by putamen–cortex and pallidum-cortex had an increment in deep gray matter-cortex during MS progress. In addition, pallidum and paracentral lobule are among the regions that contribute to human movement. According to the symptoms of MS, the mentioned regions demonstrate segments of the brain, which affect the MS patients’ movement throughout the disorder. Dysmetria, or lack of coordination of movement, is prevalent among MS patients that might be related to the mentioned regions.
It is thought that the cuneus is involved in visual processing, and is also modulated to extra-retinal effects, like attention and visual processing. Droby et al. (2016) also reported that the cuneus is involved in MS as a damaged region. Zurita et al. (2018) demonstrated that the cuneus is an effective region in RRMS in an MRI study. The postcentral gyrus was an informative region among the groups. This finding is consistent with several previous studies. For example, Sbardella et al. (2017) reported that the mentioned region is significantly different between the MS group and healthy individuals in a multi-modal MRI study. In another study, Cirillo et al. (2016) found that the resting-state connectivity increased in MS patients between the left precentral and postcentral gyrus using MRI. Tavazzi et al. (2018) also reported a decreased activation relevant to the motor task and an increment of functional connectivity in the precentral and post-central gyrus, bilaterally via fMRI in a neurorehabilitation test of MS patients.
The cerebellum is one of the significant parcels of the brain, which is involved in MS disorder. Cirillo et al. (2016) reported that resting-state functional connectivity of the cerebellum changes as nuclei in MRI images of MS patients. Parmar et al. (2018) also stated that the cerebellum has dysfunctions during MS progress. Weier et al. (2015) stated that progressive MS has extensive cortical demyelination in the cerebellum, which was revealed by MRI and is in line with our study. Ashtiani et al., (2018) also found this region to be discriminative among RRMS patients and HCs.
5. Conclusion
We extracted functional connectivity network measures derived from fMRI data of early MS patients and healthy subjects during a specific cognitive task by applying the graph theory via a non-linear connectivity measure. Wilcoxon rank-sum test was employed to find the discriminative features as biomarkers of MS. In addition, classification was performed on the discriminative features using the proposed hybrid feature selection method. Several regions, including the hippocampus, parahippocampal region, cuneus, and pallidum, and two segments of the cerebellum were discriminative in local measures. Almost all these regions were the same in different centrality measures. Moreover, combining the outputs of the Wilcoxon rank-sum test and Fisher score as a hybrid method led to a superior classification result (accuracy=95%), which outperformed the same procedure of analysis using MI (accuracy=90%) and Pearson’s correlation coefficient (accuracy=85%). In conclusion, we believe that non-linear connectivity measures, like KMI, outperform linear connectivity measures, like correlation coefficient in finding the biomarkers of MS disease according to classification performance metrics.
Ethical Considerations
Compliance with ethical guidelines
There were no ethical considerations to be considered in this research.
Funding
This research did not receive any grant from funding agencies in the public, commercial, or non-profit sectors.
Authors' contributions
All authors equally contributed to preparing this article.
Conflict of interest
The authors declared no conflict of interest.
References
Acharya, U. R., Vidya, K. S., Ghista, D. N., Lim, W. J. E., Molinari, F., & Sankaranarayanan, M. (2015). Computer-aided diagnosis of diabetic subjects by heart rate variability signals using discrete wavelet transform method. Knowledge-Based Systems, 81, 56-64. [DOI:10.1016/j.knosys.2015.02.005]
Afshani, F., Shalbaf, A., Shalbaf, R., & Sleigh, J. (2019). Frontal-temporal functional connectivity of EEG signal by standardized permutation mutual information during anesthesia. Cognitive Neurodynamics, 13(6), 531–540. [PMID] [PMCID]
Ahmadi, A., Davoudi, S., Behroozi, M., & Daliri, M. R. (2020). Decoding covert visual attention based on phase transfer entropy. Physiology & Behavior, 222, 112932. [DOI:10.1016/j.physbeh.2020.112932] [PMID]
Ahmadi, A., Davoudi, S., & Daliri, M. R. (2019). Computer Aided Diagnosis System for multiple sclerosis disease based on phase to amplitude coupling in covert visual attention. Computer Methods and Programs in Biomedicine, 169, 9–18.[DOI:10.1016/j.cmpb.2018.11.006] [PMID]
Ahmadi, H., Fatemizadeh, E., & Motie-Nasrabadi, A. (2020). fMRI functional connectivity analysis via kernel graph in Alzheimer’s disease. Signal, Image and Video Processing, 15, 1-9. [DOI:10.1007/s11760-020-01789-y]
Ashtiani, S. N. M., Daliri, M. R., Behnam, H., Hossein-Zadeh, G.A., Mehrpour, M., & Motamed, M. R., et al. (2018). Altered topological properties of brain networks in the early MS patients revealed by cognitive task-related fMRI and graph theory. Biomedical Signal Processing and Control, 40, 385-395. [DOI:10.1016/j.bspc.2017.10.006]
Azarmi, F., Miri Ashtiani, S. N., Shalbaf, A., Behnam, H., & Daliri, M. R. (2019). Granger causality analysis in combination with directed network measures for classification of MS patients and healthy controls using task-related fMRI. Computers in Biology and Medicine, 115, 103495. [DOI:10.1016/j.compbiomed.2019.103495] [PMID]
Baltruschat, S. A., Ventura-Campos, N., Cruz-Gómez, Á. J., Belenguer, A., & Forn, C. (2015). Gray matter atrophy is associated with functional connectivity reorganization during the Paced Auditory Serial Addition Test (PASAT) execution in Multiple Sclerosis (MS). Journal of Neuroradiology, 42(3), 141–149. [DOI:10.1016/j.neurad.2015.02.006] [PMID]
Beirlant, J., Dudewicz, E. J., Gyor, L., & Van der Meulen, E. C. (1997). Nonparametric entropy estimation: An overview. International Journal of Mathematical and Statistical Sciences, 6(1), 17-39. [Link]
Boutière, C., Rey, C., Zaaraoui, W., Le Troter, A., Rico, A., & Crespy, L., et al. (2017). Improvement of spasticity following intermittent theta burst stimulation in multiple sclerosis is associated with modulation of resting-state functional connectivity of the primary motor cortices. Multiple Sclerosis, 23(6), 855–863. [DOI:10.1177/1352458516661640] [PMID]
Cassidy, B., Rae, C., & Solo, V. (2015). Brain activity: Connectivity, sparsity, and mutual information. IEEE Transactions on Medical Imaging, 34(4), 846–860. [DOI:10.1109/TMI.2014.2358681] [PMID]
Charil, A., Dagher, A., Lerch, J. P., Zijdenbos, A. P., Worsley, K. J., & Evans, A. C. (2007). Focal cortical atrophy in multiple sclerosis: Relation to lesion load and disability. NeuroImage, 34(2), 509–517. [DOI:10.1016/j.neuroimage.2006.10.006] [PMID]
Chen, X., Zhang, J., Kong, D., Chen, W., & Zheng, J. (2018). Abnormal intrinsic functional hubs in relapsing-remitting multiple sclerosis: Evidence from a voxel-wise degree centrality analysis. Neuropsychiatry, 8(2), 448-459. [DOI:10.4172/Neuropsychiatry.1000366]
Cirillo, S., Rocca, M. A., Ghezzi, A., Valsasina, P., Moiola, L., & Veggiotti, P., et al. (2016). Abnormal cerebellar functional MRI connectivity in patients with paediatric multiple sclerosis. Multiple Sclerosis, 22(3), 292–301. [DOI:10.1177/1352458515592191] [PMID]
Cohen, M. X. (2014). Analyzing neural time series data: Theory and practice. Cambridge: MIT press. [DOI:10.7551/mitpress/9609.001.0001]
Cover, T. M., & Thomas, J. A. (2012). Elements of information theory. Hoboken: John Wiley & Sons. [Link]
Cui, F., Zhou, L., Wang, Z., Lang, C., Park, J., & Tan, Z., et al. (2017). Altered functional connectivity of striatal subregions in patients with multiple sclerosis. Frontiers in Neurology, 8, 129. [DOI:10.3389/fneur.2017.00129] [PMID] [PMCID]
Deshpande, G., LaConte, S., Peltier, S., & Hu, X. (2006). Connectivity analysis of human functional MRI data: From linear to nonlinear and static to dynamic. Paper presented at The International Workshop on Medical Imaging and Virtual Reality. Shanghai, China; 18 August 2006. [DOI:10.1007/11812715_3]
Dimitriadis, S. I., Simos, P. G., Fletcher, J. Μ., & Papanicolaou, A. C. (2018). Aberrant resting-state functional brain networks in dyslexia: Symbolic mutual information analysis of neuromagnetic signals. International Journal of Psychophysiology, 126, 20–29. [DOI:10.1016/j.ijpsycho.2018.02.008] [PMID]
Droby, A., Yuen, K. S., Muthuraman, M., Reitz, S. C., Fleischer, V., & Klein, J., et al. (2016). Changes in brain functional connectivity patterns are driven by an individual lesion in MS: A resting-state fMRI study. Brain Imaging and Behavior, 10(4), 1117–1126. [DOI:10.1007/s11682-015-9476-3] [PMID]
Duda, R. O., Hart, P. E., & Stork, D. G. (2012). Pattern classificatio. Hoboken: John Wiley & Sons. [Link]
Eijlers, A. J., Meijer, K. A., Wassenaar, T. M., Steenwijk, M. D., Uitdehaag, B. M., & Barkhof, F., et al. (2017). Increased default-mode network centrality in cognitively impaired multiple sclerosis patients. Neurology, 88(10), 952–960. [DOI:10.1212/WNL.0000000000003689] [PMID]
Faivre, A., Robinet, E., Guye, M., Rousseau, C., Maarouf, A., & Le Troter, A., et al. (2016). Depletion of brain functional connectivity enhancement leads to disability progression in multiple sclerosis: A longitudinal resting-state fMRI study. Multiple Sclerosis, 22(13), 1695–1708. [DOI:10.1177/1352458516628657] [PMID]
Farahani, F. V., Karwowski, W., & Lighthall, N. R. (2019). Application of graph theory for identifying connectivity patterns in human Brain networks: A systematic review. Frontiers in Neuroscience, 13, 585 [DOI:10.3389/fnins.2019.00585] [PMID] [PMCID]
Gamboa, O. L., Tagliazucchi, E., von Wegner, F., Jurcoane, A., Wahl, M., & Laufs, H., et al. (2014). Working memory performance of early MS patients correlates inversely with modularity increases in resting state functional connectivity networks. NeuroImage, 94, 385–395. [DOI:10.1016/j.neuroimage.2013.12.008] [PMID]
Gong, A., Liu, J., Chen, S., & Fu, Y. (2018). Time-frequency cross mutual information analysis of the brain functional networks underlying multiclass motor imagery. Journal of Motor Behavior, 50(3), 254–267. [DOI:10.1080/00222895.2017.1327417] [PMID]
Heinzle, J., Koopmans, P. J., den Ouden, H. E. M., Raman, S., & Stephan, K. E. (2016). A hemodynamic model for layered BOLD signals. NeuroImage, 125, 556–570. [DOI:10.1016/j.neuroimage.2015.10.025] [PMID]
Jenkinson, M., Bannister, P., Brady, M., & Smith, S. (2002). Improved optimization for the robust and accurate linear registration and motion correction of brain images. NeuroImage, 17(2), 825–841. [DOI:10.1006/nimg.2002.1132] [PMID]
Jenkinson, M., & Smith, S. (2001). A global optimisation method for robust affine registration of brain images. Medical Image Analysis, 5(2), 143–156. [DOI:10.1016/S1361-8415(01)00036-6] [PMID]
Karanikolas, G., Giannakis, G. B., Slavakis, K., & Leahy, R. M. (2016). Multi-kernel based nonlinear models for connectivity identification of brain networks. Paper presented at the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Shanghai, China; 19 May 2016. [DOI:10.1109/ICASSP.2016.7472892]
Kern, K. C., Gold, S. M., Lee, B., Montag, M., Horsfall, J., & O'Connor, M. F., et al. (2014). Thalamic-hippocampal-prefrontal disruption in relapsing-remitting multiple sclerosis. NeuroImage. Clinical, 8, 440–447. [DOI:10.1016/j.nicl.2014.12.015] [PMID] [PMCID]
Khazaee, A., Ebrahimzadeh, A., & Babajani-Feremi, A. (2015). Identifying patients with alzheimer's disease using resting-state fMRI and graph theory. Clinical Neurophysiology, 126(11), 2132–2141. [DOI:10.1016/j.clinph.2015.02.060] [PMID]
Khazaee, A., Ebrahimzadeh, A., Babajani-Feremi, A., & Alzheimer’s Disease Neuroimaging Initiative (2017). Classification of patients with MCI and AD from healthy controls using directed graph measures of resting-state fMRI. Behavioural Brain Research, 322(Pt B), 339–350. [DOI:10.1016/j.bbr.2016.06.043] [PMID]
Koenig, K. A., Rao, S. M., Lowe, M. J., Lin, J., Sakaie, K. E., & Stone, L., et al. (2019). The role of the thalamus and hippocampus in episodic memory performance in patients with multiple sclerosis. Multiple Sclerosis, 25(4), 574–584. [DOI:10.1177/1352458518760716] [PMID] [PMCID]
Lahaye, P. J., Poline, J. B., Flandin, G., Dodel, S., & Garnero, L. (2003). Functional connectivity: Studying nonlinear, delayed interactions between BOLD signals. NeuroImage, 20(2), 962–974. [DOI:10.1016/S1053-8119(03)00340-9] [PMID]
Li, X., Marrelec, G., Hess, R. F., & Benali, H. (2010). A nonlinear identification method to study effective connectivity in functional MRI. Medical Image Analysis, 14(1), 30–38. [DOI:10.1016/j.media.2009.09.005] [PMID]
Liu, C., Li, Y., Song, S., & Zhang, J. (2020). Decoding disparity categories in 3-dimensional images from fMRI data using functional connectivity patterns. Cognitive Neurodynamics, 14(2), 169–179. [PMID] [PMCID]
Logothetis, N. K., Pauls, J., Augath, M., Trinath, T., & Oeltermann, A. (2001). Neurophysiological investigation of the basis of the fMRI signal. Nature, 412(6843), 150–157. [DOI:10.1038/35084005] [PMID]
Miri Ashtiani, S. N., Behnam, H., Daliri, M. R., Hossein-Zadeh, G. A., & Mehrpour, M. (2019). Analysis of brain functional connectivity network in MS patients constructed by modular structure of sparse weights from cognitive task-related fMRI. Australasian Physical & Engineering Sciences in Medicine, 42(4), 921–938. [DOI:10.1007/s13246-019-00790-1] [PMID]
Mainero, C., Caramia, F., Pozzilli, C., Pisani, A., Pestalozza, I., & Borriello, G., et al. (2004). fMRI evidence of brain reorganization during attention and memory tasks in multiple sclerosis. NeuroImage, 21(3), 858–867. [DOI:10.1016/j.neuroimage.2003.10.004] [PMID]
McHugh M. L. (2012). Interrater reliability: The kappa statistic. Biochemia Medica, 22(3), 276–282. [DOI:10.11613/BM.2012.031] [PMID] [PMCID]
Meijer, K. A., Eijlers, A. J. C., Geurts, J. J. G., & Schoonheim, M. M. (2018). Staging of cortical and deep grey matter functional connectivity changes in multiple sclerosis. Journal of Neurology, Neurosurgery, and Psychiatry, 89(2), 205–210. [DOI:10.1136/jnnp-2017-316329] [PMID]
Miller, D. H., Leary, S. M., & Thompson, A. J. (2004). Overview of London trial of intramuscular interferon-beta Ia in primary-progressive multiple sclerosis. Multiple Sclerosis, 10(Suppl 1), S56–S57. [DOI:10.1177/135245850401000109] [PMID]
Mitolo, M., Venneri, A., Wilkinson, I. D., & Sharrack, B. (2015). Cognitive rehabilitation in multiple sclerosis: A systematic review. Journal of the Neurological Sciences, 354(1-2), 1–9. [DOI:10.1016/j.jns.2015.05.004] [PMID]
Moon, Y. I., Rajagopalan, B., & Lall, U. (1995). Estimation of mutual information using kernel density estimators. Physical Review, 52(3), 2318–2321. [DOI:10.1103/PhysRevE.52.2318] [PMID]
Mørch, N., Hansen, L. K., Strother, S. C., Svarer, C., Rottenberg, D. A., & Lautrup, et al. (1997). Nonlinear versus linear models in functional neuroimaging: Learning curves and generalization crossover. Paper presented at the Biennial International Conference on Information Processing in Medical Imaging. San Carlos de Bariloche, Argentina; 16 June 2023. [DOI:10.1007/3-540-63046-5_20]
Nelson, F., Akhtar, M. A., Zúñiga, E., Perez, C. A., Hasan, K. M., & Wilken, J., et al. (2017). Novel fMRI working memory paradigm accurately detects cognitive impairment in multiple sclerosis. Multiple Sclerosis, 23(6), 836–847. [DOI:10.1177/1352458516666186] [PMID] [PMCID]
Noseworthy, J. H., Lucchinetti, C., Rodriguez, M., & Weinshenker, B. G. (2000). Multiple sclerosis. The New England Journal of Medicine, 343(13), 938–952. [DOI:10.1056/NEJM200009283431307] [PMID]
Parmar, K., Stadelmann, C., Rocca, M. A., Langdon, D., D'Angelo, E., & D'Souza, M., et al. (2018). The role of the cerebellum in multiple sclerosis-150 years after Charcot. Neuroscience and Biobehavioral Reviews, 89, 85–98. [DOI:10.1016/j.neubiorev.2018.02.012] [PMID]
Polman, C. H., Reingold, S. C., Edan, G., Filippi, M., Hartung, H. P., & Kappos, L., et al. (2005). Diagnostic criteria for multiple sclerosis: 2005 revisions to the "McDonald Criteria". Annals of Neurology, 58(6), 840–846. [DOI:10.1002/ana.20703] [PMID]
Qiu, P., Gentles, A. J., & Plevritis, S. K. (2009). Fast calculation of pairwise mutual information for gene regulatory network reconstruction. Computer Methods and Programs in Biomedicine, 94(2), 177–180. [DOI:10.1016/j.cmpb.2008.11.003] [PMID]
Rocca, M. A., Barkhof, F., De Luca, J., Frisén, J., Geurts, J. J. G., & Hulst, H. E., et al. (2018). The hippocampus in multiple sclerosis. The Lancet. Neurology, 17(10), 918–926. [DOI:10.1016/S1474-4422(18)30309-0] [PMID]
Ruano, L., Portaccio, E., Goretti, B., Niccolai, C., Severo, M., & Patti, F., et al. (2017). Age and disability drive cognitive impairment in multiple sclerosis across disease subtypes. Multiple Sclerosis 23(9), 1258–1267. [DOI:10.1177/1352458516674367] [PMID]
Sandry, J., Paxton, J., & Sumowski, J. F. (2016). General mathematical ability predicts PASAT performance in MS patients: Implications for clinical interpretation and cognitive reserve. Journal of the International Neuropsychological Society, 22(3), 375–378. [DOI:10.1017/S1355617715001307] [PMID]
Sbardella, E., Upadhyay, N., Tona, F., Prosperini, L., De Giglio, L., & Petsas, N., et al. (2017). Dentate nucleus connectivity in adult patients with multiple sclerosis: Functional changes at rest and correlation with clinical features. Multiple Sclerosis, 23(4), 546–555. [DOI:10.1177/1352458516657438] [PMID]
Schmah, T., Yourganov, G., Zemel, R. S., Hinton, G. E., Small, S. L., & Strother, S. C. (2010). Comparing classification methods for longitudinal fMRI studies. Neural Computation, 22(11), 2729–2762. [DOI:10.1162/NECO_a_00024] [PMID]
Sheng, J., Wang, B., Zhang, Q., Liu, Q., Ma, Y., Liu, W., et al. (2019). A novel joint HCPMMP method for automatically classifying Alzheimer's and different stage MCI patients. Behavioural Brain Research, 365, 210–221. [DOI:10.1016/j.bbr.2019.03.004] [PMID]
Smith S. M. (2002). Fast robust automated brain extraction. Human Brain Mapping, 17(3), 143–155. [DOI:10.1002/hbm.10062] [PMID] [PMCID]
Spiteri, S., Hassa, T., Claros-Salinas, D., Dettmers, C., & Schoenfeld, M. A. (2019). Neural correlates of effort-dependent and effort-independent cognitive fatigue components in patients with multiple sclerosis. Multiple Sclerosis, 25(2), 256–266. [DOI:10.1177/1352458517743090] [PMID]
Tacchino, A., Saiote, C., Brichetto, G., Bommarito, G., Roccatagliata, L., & Cordano, C., et al. (2018). Motor imagery as a function of disease severity in multiple sclerosis: An fMRI Study. Frontiers in Human Neuroscience, 11, 628. [DOI:10.3389/fnhum.2017.00628] [PMID] [PMCID]
Tavazzi, E., Bergsland, N., Cattaneo, D., Gervasoni, E., Laganà, M. M., & Dipasquale, O., et al. (2018). Effects of motor rehabilitation on mobility and brain plasticity in multiple sclerosis: A structural and functional MRI study. Journal of Neurology, 265(6), 1393–1401. [DOI:10.1007/s00415-018-8859-y] [PMID]
Thompson, W. H., & Fransson, P. (2015). The frequency dimension of fMRI dynamic connectivity: Network connectivity, functional hubs and integration in the resting brain. NeuroImage, 121, 227–242. [DOI:10.1016/j.neuroimage.2015.07.022] [PMID]
Tommasin, S., De Giglio, L., Ruggieri, S., Petsas, N., Giannì, C., & Pozzilli, C., et al. (2018). Relation between functional connectivity and disability in multiple sclerosis: A non-linear model. Journal of Neurology, 265(12), 2881–2892. [DOI:10.1007/s00415-018-9075-5] [PMID]
Trapp, B. D., Vignos, M., Dudman, J., Chang, A., Fisher, E., & Staugaitis, S. M., et al. (2018). Cortical neuronal densities and cerebral white matter demyelination in multiple sclerosis: A retrospective study. The Lancet. Neurology, 17(10), 870–884.[DOI:10.1016/S1474-4422(18)30245-X] [PMID] [PMCID]
Vacchi, L., Rocca, M. A., Meani, A., Rodegher, M., Martinelli, V., & Comi, G., et al. (2017). Working memory network dysfunction in relapse-onset multiple sclerosis phenotypes: A clinical-imaging evaluation. Multiple Sclerosis, 23(4), 577–587. [DOI:10.1177/1352458516656809] [PMID]
van Geest, Q., Hulst, H. E., Meijer, K. A., Hoyng, L., Geurts, J. J. G., & Douw, L. (2018). The importance of hippocampal dynamic connectivity in explaining memory function in multiple sclerosis. Brain and Behavior, 8(5), e00954. [DOI:10.1002/brb3.954] [PMID] [PMCID]
Wang, Z., Alahmadi, A., Zhu, D., & Li, T. (2015). Brain functional connectivity analysis using mutual information. Paper presented at the 2015 IEEE Global Conference on Signal and Information Processing. Orlando, FL, USA; 16 December 2015. [DOI:10.1109/GlobalSIP.2015.7418254]
Weier, K., Banwell, B., Cerasa, A., Collins, D. L., Dogonowski, A. M., & Lassmann, H., et al. (2015). The role of the cerebellum in multiple sclerosis. Cerebellum, 14(3), 364–374. [DOI:10.1007/s12311-014-0634-8] [PMID]
Welton, T., Constantinescu, C. S., Auer, D. P., & Dineen, R. A. (2020). Graph theoretic analysis of brain connectomics in multiple sclerosis: Reliability and relationship with cognition. Brain Connectivity, 10(2), 95–104. [DOI:10.1089/brain.2019.0717] [PMID] [PMCID]
Wen, W., Zhu, W., He, Y., Kochan, N. A., Reppermund, S., & Slavin, M. J., et al. (2011). Discrete neuroanatomical networks are associated with specific cognitive abilities in old age. The Journal of Neuroscience, 31(4), 1204–1212. [DOI:10.1523/JNEUROSCI.4085-10.2011] [PMID] [PMCID]
Xia, M., Wang, J., & He, Y. (2013). BrainNet Viewer: A network visualization tool for human brain connectomics. Plos One, 8(7), e68910. [DOI:10.1371/journal.pone.0068910] [PMID] [PMCID]
Yang, Y., Solis-Escalante, T., Yao, J., Daffertshofer, A., Schouten, A. C., & van der Helm, F. C. (2016). A general approach for quantifying nonlinear connectivity in the nervous system based on phase coupling. International Journal of Neural Systems, 26(1), 1550031. [DOI:10.1142/S0129065715500318] [PMID]
Yourganov, G., Schmah, T., Churchill, N. W., Berman, M. G., Grady, C. L., & Strother, S. C. (2014). Pattern classification of fMRI data: Applications for analysis of spatially distributed cortical networks. NeuroImage, 96, 117–132. [DOI:10.1016/j.neuroimage.2014.03.074] [PMID]
Zhao, Y., & Zhang, Y. (2008). Comparison of decision tree methods for finding active objects. Advances in Space Research, 41(12), 1955-1959. [DOI:10.1016/j.asr.2007.07.020]
Zhao, Y., Zhao, Y., Durongbhan, P., Chen, L., Liu, J., & Billings, S. A., et al. (2020). Imaging of nonlinear and dynamic functional brain connectivity based on eeg recordings with the application on the diagnosis of alzheimer's disease. IEEE Transactions on Medical Imaging, 39(5), 1571–1581. [DOI:10.1109/TMI.2019.2953584] [PMID]
Zurita, M., Montalba, C., Labbé, T., Cruz, J. P., Dalboni da Rocha, J., & Tejos, C., et al. (2018). Characterization of relapsing-remitting multiple sclerosis patients using support vector machine classifications of functional and diffusion MRI data. NeuroImage. Clinical, 20, 724–730. [DOI:10.1016/j.nicl.2018.09.002] [PMID] [PMCID]
Multiple sclerosis (MS) is an unforeseeable sickness that disrupts the function of the central nervous system (CNS) with an inflaming mechanism. MS obstructs the flow of information within the brain and between the brain and body. It is thought that MS is the most prevalent autoimmune disease among young adults affecting the CNS, which is characterized by the development of lesions in vital nerves (Lucchinetti et al., 2000; Mitolo, 2015; Nelson et al., 2017). MS patients may experience several types of symptoms, including motor, cognitive, and neuropsychiatric disorders. In this regard, a significant number of MS patients suffer from cognitive impairment (Ruano et al., 2017). Patients experience such deficits from the beginning of the disease, which leads to permanent disability. Cognitive impairment usually involves several functions of the brain (Ruano et al., 2017) that strongly affect several aspects of patients’ personal lives, and may finally, cause the reduction of life’s overall quality. Hence, early identification of the inflammatory mechanism allows patients to start therapy with an immunomodulatory agent well before receiving a clinical diagnosis of definitive MS, thus slowing the degenerative advancement of MS (Miller, 2004).
Tissue damage is prevalent among MS patients. If the compensatory brain processes cannot counter tissue damage, MS may enter the irreversible disability phase. Accordingly, functional magnetic resonance imaging (fMRI), as a promising modality, reveals the brain’s functional network reorganization when the compensatory processes are still efficient at the initial phases of the disease. Therefore, fMRI can be utilized for diagnosis in the initial phases of the disease. In this regard, blood oxygen level-dependent (BOLD) can record the data (Faivre et al., 2016). Specific tasks may be practical for the activating cognitive functions of the brain in fMRI sessions, among which the paced auditory serial addition test (PASAT) is prominent for the case of MS disease. Multiple cognitive domains are measured using PASAT (Sandry et al., 2016). As a result, the gray matter atrophy in MS is related to functional connectivity reorganization during the PASAT implementation (Baltruschat et al., 2015).
The performance of the human brain in a particular task is associated with the brain network. In recent studies, analysis of the brain networks through connectivity is of great concern. Brain connectivity analysis is an eminent concept for obtaining information from the cerebral network’s neural organization and assessing the brain’s performance. One well-known non-linear functional connectivity method is mutual information (MI), which led to reliable results in previous studies (Cassidy et al., 2014; Dimitriadis et al., 2018; Thompson & Fransson, 2015). According to the non-linear nature of the BOLD time series (Heinzle et al., 2016; Logothetis et al., 2001), MI is more likely to provide reliable results rather than linear connectivity measures. In addition, MI offers invaluable information about the linear properties of the data as well (Cohen, 2014). Several studies have analyzed fMRI or EEG data using MI to investigate the brain. For instance, Dimitriadis et al., (2018) used symbolic MI and showed that impaired children demonstrate a less effective network compared with healthy subjects in terms of cross-frequency interactions between brain regions. Gong et al. (Gong et al., 2018) used MI to study the physiologic pattern of motor imagery in four tasks. Cassidy et al. (Cassidy et al., 2014) used partial coherence obtained by sparse vector autoregressive (VAR) models to calculate the MI. However, MI has a potential drawback in that it is sensitive to the number of selected bins (Cohen, 2014). Moreover, MI is based on histograms, which are discontinuous, and may provide erroneous results due to the continuous nature of neural time series. Kernel MI (KMI) is a consistent method that does not have the drawbacks of MI. This method is insensitive to the choice of the origin, and more complicated window shapes may be conducted. Furthermore, it provides an enhanced mean square error in converging the estimation of the data. Therefore, KMI outperforms MI in terms of neural data analysis (Moon et al., 1995). In this regard, Wang et al. (2015). demonstrated that MI estimation using kernel functions is consistent with the symptoms of Alzheimer’s disease (AD).
One of the most intricate networks discovered is the human brain. In this regard, roughly 86 billion neurons allow the transmission of electrical and chemical signals in the brain. It is widely assumed that the graph theory development establishes a fundamental framework for gaining a deep comprehension of the brain, and provides exquisite insights into the biological process of the human brain in cognition (Farahani et al., 2019). There have been few studies on the brain network of MS patients. For example, graph theory was implemented via resting-state fMRI to assess alteration in the brain networks among relapsing-remitting MS (RRMS) patients and healthy controls and the results demonstrated that the efficiency decreased in RRMS individuals. Also, the mean connectivity strength identified RRMS subjects and clinically isolated syndrome (CIS) individuals from healthy subjects with a 77% accuracy in each category (Liu et al., 2017). Ashtiani et al., (2018) also used graph theory for assessing MS disease. They reported several informative regions between healthy and MS subjects. They also discovered that small worldness and clustering coefficient were greater in healthy controls (HCs) compared to RRMS patients. Welton et al. (2020) used multiple cognitive tasks to test the reliability of network measures in predicting cognitive performance. They showed that damaged network structures can predict cognitive impairment in MS and that monitoring is accurate for one month.
The present study aimed to evaluate the alteration in brain network based on a non-linear connectivity measure using cognitive task-fMRI data between MS patients at initial phases and HCs. In this regard, discriminative graph measures and informative regions must be specified using a prominent statistical test. Moreover, the particular features for data classification must be chosen. Hence, a robust method for feature selection and classification must be proposed. According to the literature, no research used KMI via task data to present cognitive impairment in MS patients using graph measures. Hence, we conducted KMI in this study and constructed a graph network using the results of connectivity analysis using BOLD fMRI data, and used PASAT in the experimentation to activate cognitive functions of the brain. The brain time series was extracted from each region using automated anatomical labeling (AAL) atlas. Afterward, network measures in each subject were extracted. The best size of the kernel window was found using searching over a wide range of kernel widths according to the best result of the classification section. Then, a between-class significance test was implemented on the data between patients and HCs. The classification was employed on the results using different hyperparameters of the decision tree and support vector machine (SVM). The results obtained in the present study were compared with the previous study with the same data (Ashtiani et al., 2018) using classification performance metrics.
2. Materials and Methods
Dataset description
Twenty subjects participated in the present study, including eight patients (seven women and one man) in the initial phases, and 12 HCs (eight women and four men). All participants were right-handed, determined by McDonald’s criteria (Polman et al., 2005). The patients suffered from RRMS. All patients were between 26 and 44 years old. Patients were diagnosed an average of 30 months before the trial (ranging from 8 to 60 months). HCs were between 23 to 40 years old with a mean age of 30.67. The expanded disability status scale (EDSS) score was below 3.5 for patients. This means patients had a minimal physical disability and were in the initial phases. It is essential to note that patients with <5 years of diagnosis of the disease were chosen for this study. Furthermore, the participants filled out a consent form before the experiment. The patients were not in the attack phase during the experimental procedure, and at least three weeks had passed since the last hospitalization for the experiment.
Experimental paradigm
PASAT was used to test memory, executive functioning, and information processing as cognitive functions. The modified version of the PASAT was used in this study. In the original version, a digit between 0 and 9 is played every 3 seconds using an audio headset, and the participant has to press a response box key if the summation of two sequential numbers is below ten, while they have to prevent doing such action, otherwise. The summation number was altered to 11 in this experiment, and the language of the test was Persian. We used the block design to conduct the experiment by implementing the active and rest stages. The duration of each stage was 30 seconds. In the active stage, the participants had to perform the PASAT procedure. However, they had to close their eyes in the resting stage and try to think about nothing. The total duration of the experiment was 6 minutes, including six times at each stage. As a result, 12 phases were employed in the experimentation of each subject.
In this experiment, a 3 Tesla Siemens Tim Trio system was employed to obtain structural and functional MRI images. Echo planar imaging (EPI) was used for functional images (repetition time 2 s, echo time=30 ms, field of view=192 mm2, and flip angle=90°) and the structural images were constructed by means of a high-resolution T1-weighted MPRAGE pulse sequence (repetition time=1.8 s, echo time=3.44 ms, flip angle=7° ). A detailed description of the experimental paradigm can be found in a previous study (Ashtiani et al., 2018).
Data analysis pipeline
The procedure of data analysis is illustrated in Figure 1. A hybrid feature selection method was implemented in the present study using the Wilcoxon rank-sum test with the Fisher score. The same procedure has been repeated using the correlation and MI-based network to compare the classification results of the correlation and MI-based networks and KMI-based networks.

Preprocessing
FEAT fMRI analysis was used to conduct preprocessing on FSL (FMRIB’s Software Library). The preprocessing pipeline is demonstrated in Figure 2. MCFLIRT, BET, and FLIRT (Jenkinson et al., 2002; Jenkinson & Smith, 2001; Smith, 2002) options were used to implement the preprocessing stage. The detailed steps of preprocessing are described in a previous study (Ashtiani et al., 2018).

Brain network construction via kernel estimation of MI
Neuroimaging studies often require dividing the brain into parcels (regions) with homogenous properties The AAL atlas was utilized in order to parcellate the brain into 116 regions of interest (ROIs). The averaging method was implemented to obtain the signal of each parcel. The brain connectivity of each pair of parcels was determined after the signals of regions were extracted. Having two signals, X and Y, the MI between X and Y is defined as Equation 1:
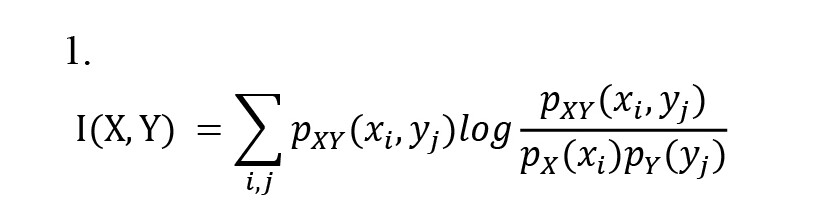
Where, px(x) is the marginal probability of X and py(y) is the marginal probability Y. Also pxy(x, y) is the joint probability of X and Y. The probability values in the above statement are estimated by binning the distributions and creating a histogram (Cover & Thomas, 2012). KMI, however, applies the Gaussian kernel function rather than binning the distribution (Beirlant et al., 1997). The Equations 2, 3, 4 statements show the probabilities employed using Gaussian kernel functions:

Here, h is a parameter for controlling the width of the kernel, which is defined based on σ, the standard deviation of the kernel. KMI can be used as a functional connectivity method, in which interdependence between regions is extracted. KMI can be defined as Equation 5:

We used each brain’s whole time series as X and Y and constructed connectivity matrices for all of the subjects using KMI in the whole 12 phases of active and rest. Therefore, the brain network of each subject will be constructed. Assuming σ as the standard deviation of the Gaussian kernel, various standard deviations, including 2, 1.5, 1, 0.5, 0.25, and 0.125, were used in this method. However, we considered σ equal to 0.25 for reporting the results since the best classification accuracy was achieved in such a condition. We considered each ROI as a node and measures of connectivity as edges of a graph for each subject and constructed the connectivity matrices. The KMI was employed using FastPairMI.m for extracting the connectivity matrices (Qiu et al., 2009).
Thresholding and extracting the graph measures
Thresholding, selecting the most consistent set of edges that jointly construct the graph, is a typical analysis stage in forming a functional graph. Each subject’s network is different from other numbers and weighs on the edges (Wen et al., 2011). Proportional thresholding (PTh) is a prominent matching strategy prior to statistical and machine learning implementations. In this approach, a specified number of the most robust connections are chosen as network edges to ensure equal network density across participants’ brain networks (Gamboa et al., 2014). The PTh method was used in this study in the range of 0.06 to 0.3 with steps equal to 0.01 to threshold the adjacency matrices. Then, each of the resulting matrices was transformed into binary. Afterward, we extracted brain graph measures from binary matrices. Using the BrainNet viewer, Figure 3 displays the full mesh graph and threshold network of a single subject at a PTh value equal to 0.19 (Xia et al., 2013).

Brain networks are commonly described using graph theory measures to show the properties of the brain structure. It is widely assumed that the brain’s substrate is a complex network. This concept is represented through several graph measures in this study. Accordingly, assortativity, characteristic path length, global efficiency, mean clustering coefficient, modularity, and transitivity were used as global measures. In addition, the betweenness centrality, degree, eigenvector centrality, k-coreness centrality, PageRank centrality, participation coefficient, and sub-graph centrality were employed as local measures.
Significance test, feature ranking, and classification
Comparing two groups is a prevalent type of scientific experimentation The Wilcoxon rank-sum test is a well-known nonparametric test for non-normal distributions, which was the case for the obtained graph measures. This test was applied to the extracted graph measures (P<0.05). The criterion for considering a measure as discriminating was that it was statistically significant at more than 12 threshold numbers (approximately half the range) in each global measure or measurement area for local measures.
Significant features were considered as the input of the feature ranking method. Multiple feature ranking methods were employed on graph measures, yet none was as robust as the Fisher score. Fisher score is a feature selection algorithm independent of class distribution that can specify the distinction power of each feature between the classes (Duda et al., 2012). The best combination of discriminative features was selected using the Fisher score by ranking the features. Afterward, we selected various combinations of the best features ranging from 1 to 10 to avoid overfitting regarding the sample size. These features were used for classification using different parameters of SVM and the decision tree. The optimal feature set is the combination, by which the highest accuracy could be obtained (Acharya et al., 2015; Ahmadi et al. 2020; Ahmadi et al., 2019). Fisher score was used within the leave-one-subject-out-cross validation (LOOCV) to avert interdependency. In other words, the Fisher score was implemented on the training set in each fold separately, and the selected features were then used on the test data in that fold. Standard performance metrics of classification, such as accuracy, sensitivity, specificity, as well as Cohen’s kappa coefficient were employed in this study. In this regard, Cohen’s kappa measures the agreement among two raters that classify N items into C mutually individual categories. This measure is strongly recommended when the labels are imbalanced. The rate of agreement categorization is previously discussed (McHugh, 2012).
3. Results
We obtained the graph features of the brain by constructing the networks via KMI. The statistical test was then used between the groups to obtain informative regions and discriminative features. Afterward, we used a combination of a statistical test and feature ranking as a hybrid feature selection method.
Hypothesis testing of global features
Altered global measures between the two groups can demonstrate changes in networks and the topology of the brain. In this study, significant values were not obtained in such measures. Table 1 demonstrates the lowest P in each measure and the corresponding PTh.

Hypothesis testing of local features
Damaged areas can alter brain topology and subsequently change local properties obtained from the mentioned areas. The degree, k-coreness centrality, betweenness centrality, participation coefficient, eigenvector centrality, PageRank centrality, and subgraph centrality were discriminative within several areas. Such measures and their corresponding informative regions are listed in Table 2.

The P and the corresponding threshold are reported for each region. Figure 4 also shows all discriminative regions.

Classification performance
Based on the Fisher score, we picked the best combination of features from 1-10 features for each classification method in order to avoid overtraining. The highest classification outcome investigated by the optimum parameters of each classifier via the graph measures of KMI-based networks is shown in Table 3.

Radial basis function SVM (RBF-SVM) had the greatest accuracy (95%) (PTh=0.09). The accuracy of RBF-SVM (PTh=0.09) in different combinations of measures is shown in Figure 5. The corresponding procedures were implemented using correlation coefficient and MI for comparison, and the results are reported in Tables 4 and 5 respectively. The best classification accuracy using the correlation coefficient and MI-based method were 85% and 90%, respectively.

The most repeated measures selected using the Fisher score using correlation-based networks were left Fusiform in degree and PageRank centrality as well as left hippocampus and left parahippocampal in k-coreness centrality, yet the most repeated measures selected using the Fisher score in KMI-based networks were left Pallidum in degree, eigenvector centrality, k-coreness centrality, and PageRank centrality as well as left parahippocampal in eigenvector centrality, k-coreness centrality, and PageRank centrality.

The corresponding measures for MI were the right hippocampus in betweenness centrality and the left pallidum in eigenvector centrality.

Significance test on connectivity
The significant difference in connectivity matrices was achieved using the Wilcoxon rank-sum test (P<0.05, FDR corrected). The number of significant connections was 3446 without FDR correction. However, this value decreased to five via FDR correction. The connectivity measure between the left medial orbitofrontal cortex and right cuneus, right middle occipital gyrus, left postcentral gyrus and, right crus I of the cerebellar hemisphere and right cuneus and right crus I of the cerebellar hemisphere were significantly different. Figure 6 also shows the significant connections in a brain sample.

Classification accuracy and feature selection of connectivity
The method for classifying connectivity values is the same as the process for classifying network measures. The Wilcoxon rank-sum test was used to derive the discriminative connectivity values. Then, we used the Fisher score to classify the data by using LOOCV. Tables 6, 7, 8 show the best classification outcome for connectivity measures.

The findings suggest that in terms of classification, connectivity values are not as reliable as network measures. However, Liu et al., (2017) mentioned that functional connectivity is a more discriminatory method than traditional activity patterns in an fMRI study.


4. Discussion
The present study aimed to assess the brain graph’s alteration in the early phases of MS compared to a healthy brain, primarily to assess the cognitive effects of the disease. Hence, we used fMRI during the performance of PASAT to analyze the brain network of MS patients compared to HCs. The classification was implemented to test the validity of the discriminative graph measures.
It is widely assumed that the BOLD fMRI time series contains non-linear properties. Accordingly Lahaye et al. (2003) found that connectivity measures obtained from the BOLD fMRI time series are unlikely to contain only linear instantaneous information. As a result, a non-linear connectivity measure was employed in this study for constructing subjects’ brain networks. Non-linear connectivity measures have superior performance over linear measures (Deshpande et al., 2006; Karanikolas et al., 2016; Li et al., 2010). In addition, Zhao et al. (2020) demonstrated the excellent performance of non-linear connectivity analysis in an electroencephalogram (EEG) study. Yang et al. (2016) also proved that the incorporation of higher-order non-linearities offers a complete inference of the phase coupling. Using a kernel function, as a non-linear approach, has a promising result in the network analysis of AD by Ahmadi et al. (2020), and leads to a robust distinction between HCs and patients in fMRI analysis. Non-linear connectivity measures, like KMI, outperform linear measures using EEG data (Afshani et al., 2015).
Several centrality measures, including the degree, PageRank centrality, eigenvector centrality, subgraph centrality, and k-coreness centrality, were discriminative in almost the same regions. Central nodes are the most critical nodes of the graph in terms of interaction with other nodes, which can be demonstrated as the degree of a node in the simplest form. In other words, most centrality measures demonstrate the amount of node participation in short paths. Many studies have assessed the brain in terms of centrality measures in MS; for example, Eijlers et al., 2017 found that several regions showed altered degree and eigenvector centrality in cognitively impaired MS patients. The obtained regions were remarkably in line with our found regions. The PageRank centrality is similar to the eigenvector centrality, including a damping factor on contributing neighbors. Ashtiani et al., 2018 reported that the PageRank centrality altered in the hippocampus and segments of the cerebellum between the MS group and HCs. They also discovered that the sub-graph centrality, a graph measure that describes the contribution of every node in all subgraphs, was altered between MS patients and controls in the hippocampal, parahippocampal, postcentral, and cerebellar regions as well. The k-coreness centrality was assessed in AD several times previously, which resembles MS as to the cognitive effects of the disease. Khazaee et al. (2017) found that the k-coreness centrality is a relatively robust feature in identifying AD patients in resting-state fMRI. Sheng et al. (2019) also used the k-coreness for training a novel human connectome project multi-modal parcellation (HCPMMP) method in classifying MS patients from HCs. Ashtiani et al., (2018) also found that the k-coreness centrality is informative in MS.
In this study, merging the Wilcoxon rank-sum test with the Fisher score, as a hybrid approach, led to superior accuracy. According to our previous study (Azarmi et al., 2019) and the achieved results, it stands to reason that when the outputs of the Wilcoxon rank-sum test are used as the input of the Fisher score, greater accuracy may be obtained rather than using the Fisher score alone. The most particular features are elected using the Fisher score from the discriminative features via the mentioned approach. As a result, the obtained features are the most independent ones for classification.
The non-linearity of classification systems is an essential aspect of the present research. In non-linear classification, the boundary for separating categories is much more complex than in linear systems. Therefore, non-linear classification, as opposed to linear classification, is more flexible and less biased (Mørch et al., 1997). Accordingly, the RBF-SVM outperformed linear SVM based on our findings. In an fMRI study, Schmah et al. (2010) reported that non-linear classifiers, like RBF-SVM or second-degree polynomial SVM, outperformed linear SVM due to changes in brain connectivity. In another study, Yourganov et al. (2014) also reported that the results could be used for a wide range of connectivity deficit studies. MS is also a neurodegenerative disease that causes connectivity deficits in the brain’s connections. The decision tree was another classification method, which was used in this study. Zhao and Zhang, (2008) reported that decision trees are unstable, and a minor difference in the training data will lead to different attribute selections at each choice point in the tree. As a result, a significant impact may occur, since attribute choices influence all descendent subtrees. The decision tree performed better than linear SVM, yet it had a lower accuracy compared to RBF-SVM based on our results. It is worth noticing that the graph features picked using the proposed feature selection approach varied from those selected using correlation and MI with KMI-based networks.
The decision tree had a greater sensitivity compared to RBF-SVM. It is thought that identifying patients correctly is crucial in neuroscientific studies rather than HCs. In other words, detecting patients as HCs is a critical limitation in such studies. As a result, the decision tree might be a superior classification system compared to RBF-SVM from this perspective. The specificity of SVM in both kernels was 100%, which is consistent with our previous research (Azarmi et al., 2019).
According to Duda et al., (2012), when the data’s dimensionality is staggering, the Fisher score is one of the most prominent feature selection techniques. We implemented various methods of feature selection but finally, the Fisher score was selected. Thus, the accuracy of classification showed a prominent value. Khazaee et al. (2015) also used various feature selection methods and gained the best accuracy using fisher score in a resting-state fMRI study, which aligns with our results. It is worth mentioning that the present study aimed to determine the discriminative network measures and informative ROIs, which could classify HCs from MS patients. Moreover, dimensionality reduction methods convert the space of the features to another space. Hence, implementing the mentioned methods would not benefit us in gaining promising results.
Cohen’s kappa is a popular statistic for inter-rater and intra-rater checking in reliability (McHugh, 2012). According to the results, RBF-SVM and decision tree were in perfect agreement using the measures of KMI-based networks, and linear SVM was in substantial agreement. In addition, linear SVM was in perfect agreement using MI-based networks. However, all classification systems were in substantial agreement with the measures of correlation-based networks. The results showed that KMI outperforms the correlation coefficient as a measure of connectivity using a prominent classification metric.
The results obtained from KMI showed a more remarkable performance in accuracy, sensitivity, specificity, and Cohen’s kappa compared to the correlation coefficient. Accordingly, KMI can be considered a valid measure of connectivity over linear measures, like the correlation coefficient. Overall, the results are expected according to the non-linear properties of KMI as well as the BOLD time series. Additionally, KMI does not have the drawbacks of MI, which is choosing the origin in binning and discontinuity. Moreover, it is computationally less complex than mode-based effective methods. Therefore, KMI is preferred to the mentioned methods. However, it is thought that multiple studies should be implemented on brain data in order to gain valid results.
Parahippocampal and pallidum regions were among the regions that were selected multiple times using the Fisher score. These regions were obtained several times in graph measures obtained by KMI or correlation coefficient. The function of the parahippocampal region is memory encoding and retrieval. Therefore, it can be assumed that this region is related to cognitive functions. Pallidum was chosen only via the KMI method and is related to voluntary movement. The hippocampus and fusiform were repeated several times using the correlation coefficient. The former plays a crucial role in memory functions, while the latter is related to word and face recognition. Both of these regions’ tasks are related to cognitive function.
Twelve ROIs were identified as discriminative regions in various local graph measures, and each of these regions has a particular functionality. All mentioned regions were associated with the impacts of MS, which are described in detail in the following sections.
Regions 14 and 16 of the AAL atlas were discriminative solely in participation coefficient and betweenness centrality, respectively. In this regard, the triangular part of the right inferior frontal gyrus is related to the go/no go task, which is significantly different in our study. A powerful response, like pressing a button or preventing performing such an action must be banned in this task. Accordingly, the go/no go task is similar to PASAT. Hence, we believe that this region might be involved in causing MS disease. Mainero et al. (2004) also reported a significant difference in the activation of this area among MS individuals and HCs while performing a recall task using fMRI data. The orbital part of the inferior frontal gyrus is also reported to be involved in causing autism, which is a neurodevelopmental disorder as well. Charil et al. (2007) reported an alteration in the thickness of the inferior frontal gyrus in RRMS patients. Trapp et al. (2018) also reported that demyelination and neuronal loss would happen in this area during MS progress. Chen et al. (2018) reported a significant difference in seed-based functional connectivity between the MS group and HCs in this region.
The hippocampus in both hemispheres of the brain and the parahippocampal gyrus in the right hemisphere were significantly different in our study, consistent with many previous studies (Kern et al., 2015; Koenig et al., 2018; Rocca et al., 2018; Vacchi et al., 2017; van Geest et al., 2018). The hippocampus is a critical region in transferring information from short-term to long-term memory as well as the organization of new memories from past experiences. This region is one of the first segments of the brain, which is damaged in AD. This region has a leading role in epilepsy and schizophrenia. In addition, the parahippocampal gyrus has a central role in memory encoding and recovery. These functions are of much importance when cognitive impairment occurs. The superior temporal pole was also reported as a region related to MS in other studies. For example, Vacchi et al., (2017) demonstrated that this region is involved in relapse-onset MS as a factor for memory dysfunction in the N-back task during the fMRI experiment. In another study, Tommasin et al. (2018) stated that the right superior temporal gyrus and left cerebellum VI lobule have different connectivity values between new MS patients and progressed MS patients, which means that the region contributes to MS during the progress of the disease.
One of the significant symptoms of MS patients is in movement control. The paracentral lobule is a supplementary motor area (SMA) segment, which contributes to motor functions. Four hypothesized functions are defined for SMA: The control of postural stability during stance or walking, temporal sequences of action coordination, bimanual coordination, and the initiation of internally generated as opposed to stimulus-driven movement. This region was reported to be related to MS several times in previous studies of fMRI (Boutière et al., 2017; Cui et al., 2017; Nelson et al., 2017; Spiteri, et al., 2017). It also is assumed that pallidum contributes to voluntary human movement. This region also plays a crucial role in MS. Tacchino et al. (2018) showed a negative correlation between the index of success and pallidum in RRMS patients as a function of disease severity in motor imagery. Meijer et al. (2018) also found that the connectivity attained by putamen–cortex and pallidum-cortex had an increment in deep gray matter-cortex during MS progress. In addition, pallidum and paracentral lobule are among the regions that contribute to human movement. According to the symptoms of MS, the mentioned regions demonstrate segments of the brain, which affect the MS patients’ movement throughout the disorder. Dysmetria, or lack of coordination of movement, is prevalent among MS patients that might be related to the mentioned regions.
It is thought that the cuneus is involved in visual processing, and is also modulated to extra-retinal effects, like attention and visual processing. Droby et al. (2016) also reported that the cuneus is involved in MS as a damaged region. Zurita et al. (2018) demonstrated that the cuneus is an effective region in RRMS in an MRI study. The postcentral gyrus was an informative region among the groups. This finding is consistent with several previous studies. For example, Sbardella et al. (2017) reported that the mentioned region is significantly different between the MS group and healthy individuals in a multi-modal MRI study. In another study, Cirillo et al. (2016) found that the resting-state connectivity increased in MS patients between the left precentral and postcentral gyrus using MRI. Tavazzi et al. (2018) also reported a decreased activation relevant to the motor task and an increment of functional connectivity in the precentral and post-central gyrus, bilaterally via fMRI in a neurorehabilitation test of MS patients.
The cerebellum is one of the significant parcels of the brain, which is involved in MS disorder. Cirillo et al. (2016) reported that resting-state functional connectivity of the cerebellum changes as nuclei in MRI images of MS patients. Parmar et al. (2018) also stated that the cerebellum has dysfunctions during MS progress. Weier et al. (2015) stated that progressive MS has extensive cortical demyelination in the cerebellum, which was revealed by MRI and is in line with our study. Ashtiani et al., (2018) also found this region to be discriminative among RRMS patients and HCs.
5. Conclusion
We extracted functional connectivity network measures derived from fMRI data of early MS patients and healthy subjects during a specific cognitive task by applying the graph theory via a non-linear connectivity measure. Wilcoxon rank-sum test was employed to find the discriminative features as biomarkers of MS. In addition, classification was performed on the discriminative features using the proposed hybrid feature selection method. Several regions, including the hippocampus, parahippocampal region, cuneus, and pallidum, and two segments of the cerebellum were discriminative in local measures. Almost all these regions were the same in different centrality measures. Moreover, combining the outputs of the Wilcoxon rank-sum test and Fisher score as a hybrid method led to a superior classification result (accuracy=95%), which outperformed the same procedure of analysis using MI (accuracy=90%) and Pearson’s correlation coefficient (accuracy=85%). In conclusion, we believe that non-linear connectivity measures, like KMI, outperform linear connectivity measures, like correlation coefficient in finding the biomarkers of MS disease according to classification performance metrics.
Ethical Considerations
Compliance with ethical guidelines
There were no ethical considerations to be considered in this research.
Funding
This research did not receive any grant from funding agencies in the public, commercial, or non-profit sectors.
Authors' contributions
All authors equally contributed to preparing this article.
Conflict of interest
The authors declared no conflict of interest.
References
Acharya, U. R., Vidya, K. S., Ghista, D. N., Lim, W. J. E., Molinari, F., & Sankaranarayanan, M. (2015). Computer-aided diagnosis of diabetic subjects by heart rate variability signals using discrete wavelet transform method. Knowledge-Based Systems, 81, 56-64. [DOI:10.1016/j.knosys.2015.02.005]
Afshani, F., Shalbaf, A., Shalbaf, R., & Sleigh, J. (2019). Frontal-temporal functional connectivity of EEG signal by standardized permutation mutual information during anesthesia. Cognitive Neurodynamics, 13(6), 531–540. [PMID] [PMCID]
Ahmadi, A., Davoudi, S., Behroozi, M., & Daliri, M. R. (2020). Decoding covert visual attention based on phase transfer entropy. Physiology & Behavior, 222, 112932. [DOI:10.1016/j.physbeh.2020.112932] [PMID]
Ahmadi, A., Davoudi, S., & Daliri, M. R. (2019). Computer Aided Diagnosis System for multiple sclerosis disease based on phase to amplitude coupling in covert visual attention. Computer Methods and Programs in Biomedicine, 169, 9–18.[DOI:10.1016/j.cmpb.2018.11.006] [PMID]
Ahmadi, H., Fatemizadeh, E., & Motie-Nasrabadi, A. (2020). fMRI functional connectivity analysis via kernel graph in Alzheimer’s disease. Signal, Image and Video Processing, 15, 1-9. [DOI:10.1007/s11760-020-01789-y]
Ashtiani, S. N. M., Daliri, M. R., Behnam, H., Hossein-Zadeh, G.A., Mehrpour, M., & Motamed, M. R., et al. (2018). Altered topological properties of brain networks in the early MS patients revealed by cognitive task-related fMRI and graph theory. Biomedical Signal Processing and Control, 40, 385-395. [DOI:10.1016/j.bspc.2017.10.006]
Azarmi, F., Miri Ashtiani, S. N., Shalbaf, A., Behnam, H., & Daliri, M. R. (2019). Granger causality analysis in combination with directed network measures for classification of MS patients and healthy controls using task-related fMRI. Computers in Biology and Medicine, 115, 103495. [DOI:10.1016/j.compbiomed.2019.103495] [PMID]
Baltruschat, S. A., Ventura-Campos, N., Cruz-Gómez, Á. J., Belenguer, A., & Forn, C. (2015). Gray matter atrophy is associated with functional connectivity reorganization during the Paced Auditory Serial Addition Test (PASAT) execution in Multiple Sclerosis (MS). Journal of Neuroradiology, 42(3), 141–149. [DOI:10.1016/j.neurad.2015.02.006] [PMID]
Beirlant, J., Dudewicz, E. J., Gyor, L., & Van der Meulen, E. C. (1997). Nonparametric entropy estimation: An overview. International Journal of Mathematical and Statistical Sciences, 6(1), 17-39. [Link]
Boutière, C., Rey, C., Zaaraoui, W., Le Troter, A., Rico, A., & Crespy, L., et al. (2017). Improvement of spasticity following intermittent theta burst stimulation in multiple sclerosis is associated with modulation of resting-state functional connectivity of the primary motor cortices. Multiple Sclerosis, 23(6), 855–863. [DOI:10.1177/1352458516661640] [PMID]
Cassidy, B., Rae, C., & Solo, V. (2015). Brain activity: Connectivity, sparsity, and mutual information. IEEE Transactions on Medical Imaging, 34(4), 846–860. [DOI:10.1109/TMI.2014.2358681] [PMID]
Charil, A., Dagher, A., Lerch, J. P., Zijdenbos, A. P., Worsley, K. J., & Evans, A. C. (2007). Focal cortical atrophy in multiple sclerosis: Relation to lesion load and disability. NeuroImage, 34(2), 509–517. [DOI:10.1016/j.neuroimage.2006.10.006] [PMID]
Chen, X., Zhang, J., Kong, D., Chen, W., & Zheng, J. (2018). Abnormal intrinsic functional hubs in relapsing-remitting multiple sclerosis: Evidence from a voxel-wise degree centrality analysis. Neuropsychiatry, 8(2), 448-459. [DOI:10.4172/Neuropsychiatry.1000366]
Cirillo, S., Rocca, M. A., Ghezzi, A., Valsasina, P., Moiola, L., & Veggiotti, P., et al. (2016). Abnormal cerebellar functional MRI connectivity in patients with paediatric multiple sclerosis. Multiple Sclerosis, 22(3), 292–301. [DOI:10.1177/1352458515592191] [PMID]
Cohen, M. X. (2014). Analyzing neural time series data: Theory and practice. Cambridge: MIT press. [DOI:10.7551/mitpress/9609.001.0001]
Cover, T. M., & Thomas, J. A. (2012). Elements of information theory. Hoboken: John Wiley & Sons. [Link]
Cui, F., Zhou, L., Wang, Z., Lang, C., Park, J., & Tan, Z., et al. (2017). Altered functional connectivity of striatal subregions in patients with multiple sclerosis. Frontiers in Neurology, 8, 129. [DOI:10.3389/fneur.2017.00129] [PMID] [PMCID]
Deshpande, G., LaConte, S., Peltier, S., & Hu, X. (2006). Connectivity analysis of human functional MRI data: From linear to nonlinear and static to dynamic. Paper presented at The International Workshop on Medical Imaging and Virtual Reality. Shanghai, China; 18 August 2006. [DOI:10.1007/11812715_3]
Dimitriadis, S. I., Simos, P. G., Fletcher, J. Μ., & Papanicolaou, A. C. (2018). Aberrant resting-state functional brain networks in dyslexia: Symbolic mutual information analysis of neuromagnetic signals. International Journal of Psychophysiology, 126, 20–29. [DOI:10.1016/j.ijpsycho.2018.02.008] [PMID]
Droby, A., Yuen, K. S., Muthuraman, M., Reitz, S. C., Fleischer, V., & Klein, J., et al. (2016). Changes in brain functional connectivity patterns are driven by an individual lesion in MS: A resting-state fMRI study. Brain Imaging and Behavior, 10(4), 1117–1126. [DOI:10.1007/s11682-015-9476-3] [PMID]
Duda, R. O., Hart, P. E., & Stork, D. G. (2012). Pattern classificatio. Hoboken: John Wiley & Sons. [Link]
Eijlers, A. J., Meijer, K. A., Wassenaar, T. M., Steenwijk, M. D., Uitdehaag, B. M., & Barkhof, F., et al. (2017). Increased default-mode network centrality in cognitively impaired multiple sclerosis patients. Neurology, 88(10), 952–960. [DOI:10.1212/WNL.0000000000003689] [PMID]
Faivre, A., Robinet, E., Guye, M., Rousseau, C., Maarouf, A., & Le Troter, A., et al. (2016). Depletion of brain functional connectivity enhancement leads to disability progression in multiple sclerosis: A longitudinal resting-state fMRI study. Multiple Sclerosis, 22(13), 1695–1708. [DOI:10.1177/1352458516628657] [PMID]
Farahani, F. V., Karwowski, W., & Lighthall, N. R. (2019). Application of graph theory for identifying connectivity patterns in human Brain networks: A systematic review. Frontiers in Neuroscience, 13, 585 [DOI:10.3389/fnins.2019.00585] [PMID] [PMCID]
Gamboa, O. L., Tagliazucchi, E., von Wegner, F., Jurcoane, A., Wahl, M., & Laufs, H., et al. (2014). Working memory performance of early MS patients correlates inversely with modularity increases in resting state functional connectivity networks. NeuroImage, 94, 385–395. [DOI:10.1016/j.neuroimage.2013.12.008] [PMID]
Gong, A., Liu, J., Chen, S., & Fu, Y. (2018). Time-frequency cross mutual information analysis of the brain functional networks underlying multiclass motor imagery. Journal of Motor Behavior, 50(3), 254–267. [DOI:10.1080/00222895.2017.1327417] [PMID]
Heinzle, J., Koopmans, P. J., den Ouden, H. E. M., Raman, S., & Stephan, K. E. (2016). A hemodynamic model for layered BOLD signals. NeuroImage, 125, 556–570. [DOI:10.1016/j.neuroimage.2015.10.025] [PMID]
Jenkinson, M., Bannister, P., Brady, M., & Smith, S. (2002). Improved optimization for the robust and accurate linear registration and motion correction of brain images. NeuroImage, 17(2), 825–841. [DOI:10.1006/nimg.2002.1132] [PMID]
Jenkinson, M., & Smith, S. (2001). A global optimisation method for robust affine registration of brain images. Medical Image Analysis, 5(2), 143–156. [DOI:10.1016/S1361-8415(01)00036-6] [PMID]
Karanikolas, G., Giannakis, G. B., Slavakis, K., & Leahy, R. M. (2016). Multi-kernel based nonlinear models for connectivity identification of brain networks. Paper presented at the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Shanghai, China; 19 May 2016. [DOI:10.1109/ICASSP.2016.7472892]
Kern, K. C., Gold, S. M., Lee, B., Montag, M., Horsfall, J., & O'Connor, M. F., et al. (2014). Thalamic-hippocampal-prefrontal disruption in relapsing-remitting multiple sclerosis. NeuroImage. Clinical, 8, 440–447. [DOI:10.1016/j.nicl.2014.12.015] [PMID] [PMCID]
Khazaee, A., Ebrahimzadeh, A., & Babajani-Feremi, A. (2015). Identifying patients with alzheimer's disease using resting-state fMRI and graph theory. Clinical Neurophysiology, 126(11), 2132–2141. [DOI:10.1016/j.clinph.2015.02.060] [PMID]
Khazaee, A., Ebrahimzadeh, A., Babajani-Feremi, A., & Alzheimer’s Disease Neuroimaging Initiative (2017). Classification of patients with MCI and AD from healthy controls using directed graph measures of resting-state fMRI. Behavioural Brain Research, 322(Pt B), 339–350. [DOI:10.1016/j.bbr.2016.06.043] [PMID]
Koenig, K. A., Rao, S. M., Lowe, M. J., Lin, J., Sakaie, K. E., & Stone, L., et al. (2019). The role of the thalamus and hippocampus in episodic memory performance in patients with multiple sclerosis. Multiple Sclerosis, 25(4), 574–584. [DOI:10.1177/1352458518760716] [PMID] [PMCID]
Lahaye, P. J., Poline, J. B., Flandin, G., Dodel, S., & Garnero, L. (2003). Functional connectivity: Studying nonlinear, delayed interactions between BOLD signals. NeuroImage, 20(2), 962–974. [DOI:10.1016/S1053-8119(03)00340-9] [PMID]
Li, X., Marrelec, G., Hess, R. F., & Benali, H. (2010). A nonlinear identification method to study effective connectivity in functional MRI. Medical Image Analysis, 14(1), 30–38. [DOI:10.1016/j.media.2009.09.005] [PMID]
Liu, C., Li, Y., Song, S., & Zhang, J. (2020). Decoding disparity categories in 3-dimensional images from fMRI data using functional connectivity patterns. Cognitive Neurodynamics, 14(2), 169–179. [PMID] [PMCID]
Logothetis, N. K., Pauls, J., Augath, M., Trinath, T., & Oeltermann, A. (2001). Neurophysiological investigation of the basis of the fMRI signal. Nature, 412(6843), 150–157. [DOI:10.1038/35084005] [PMID]
Miri Ashtiani, S. N., Behnam, H., Daliri, M. R., Hossein-Zadeh, G. A., & Mehrpour, M. (2019). Analysis of brain functional connectivity network in MS patients constructed by modular structure of sparse weights from cognitive task-related fMRI. Australasian Physical & Engineering Sciences in Medicine, 42(4), 921–938. [DOI:10.1007/s13246-019-00790-1] [PMID]
Mainero, C., Caramia, F., Pozzilli, C., Pisani, A., Pestalozza, I., & Borriello, G., et al. (2004). fMRI evidence of brain reorganization during attention and memory tasks in multiple sclerosis. NeuroImage, 21(3), 858–867. [DOI:10.1016/j.neuroimage.2003.10.004] [PMID]
McHugh M. L. (2012). Interrater reliability: The kappa statistic. Biochemia Medica, 22(3), 276–282. [DOI:10.11613/BM.2012.031] [PMID] [PMCID]
Meijer, K. A., Eijlers, A. J. C., Geurts, J. J. G., & Schoonheim, M. M. (2018). Staging of cortical and deep grey matter functional connectivity changes in multiple sclerosis. Journal of Neurology, Neurosurgery, and Psychiatry, 89(2), 205–210. [DOI:10.1136/jnnp-2017-316329] [PMID]
Miller, D. H., Leary, S. M., & Thompson, A. J. (2004). Overview of London trial of intramuscular interferon-beta Ia in primary-progressive multiple sclerosis. Multiple Sclerosis, 10(Suppl 1), S56–S57. [DOI:10.1177/135245850401000109] [PMID]
Mitolo, M., Venneri, A., Wilkinson, I. D., & Sharrack, B. (2015). Cognitive rehabilitation in multiple sclerosis: A systematic review. Journal of the Neurological Sciences, 354(1-2), 1–9. [DOI:10.1016/j.jns.2015.05.004] [PMID]
Moon, Y. I., Rajagopalan, B., & Lall, U. (1995). Estimation of mutual information using kernel density estimators. Physical Review, 52(3), 2318–2321. [DOI:10.1103/PhysRevE.52.2318] [PMID]
Mørch, N., Hansen, L. K., Strother, S. C., Svarer, C., Rottenberg, D. A., & Lautrup, et al. (1997). Nonlinear versus linear models in functional neuroimaging: Learning curves and generalization crossover. Paper presented at the Biennial International Conference on Information Processing in Medical Imaging. San Carlos de Bariloche, Argentina; 16 June 2023. [DOI:10.1007/3-540-63046-5_20]
Nelson, F., Akhtar, M. A., Zúñiga, E., Perez, C. A., Hasan, K. M., & Wilken, J., et al. (2017). Novel fMRI working memory paradigm accurately detects cognitive impairment in multiple sclerosis. Multiple Sclerosis, 23(6), 836–847. [DOI:10.1177/1352458516666186] [PMID] [PMCID]
Noseworthy, J. H., Lucchinetti, C., Rodriguez, M., & Weinshenker, B. G. (2000). Multiple sclerosis. The New England Journal of Medicine, 343(13), 938–952. [DOI:10.1056/NEJM200009283431307] [PMID]
Parmar, K., Stadelmann, C., Rocca, M. A., Langdon, D., D'Angelo, E., & D'Souza, M., et al. (2018). The role of the cerebellum in multiple sclerosis-150 years after Charcot. Neuroscience and Biobehavioral Reviews, 89, 85–98. [DOI:10.1016/j.neubiorev.2018.02.012] [PMID]
Polman, C. H., Reingold, S. C., Edan, G., Filippi, M., Hartung, H. P., & Kappos, L., et al. (2005). Diagnostic criteria for multiple sclerosis: 2005 revisions to the "McDonald Criteria". Annals of Neurology, 58(6), 840–846. [DOI:10.1002/ana.20703] [PMID]
Qiu, P., Gentles, A. J., & Plevritis, S. K. (2009). Fast calculation of pairwise mutual information for gene regulatory network reconstruction. Computer Methods and Programs in Biomedicine, 94(2), 177–180. [DOI:10.1016/j.cmpb.2008.11.003] [PMID]
Rocca, M. A., Barkhof, F., De Luca, J., Frisén, J., Geurts, J. J. G., & Hulst, H. E., et al. (2018). The hippocampus in multiple sclerosis. The Lancet. Neurology, 17(10), 918–926. [DOI:10.1016/S1474-4422(18)30309-0] [PMID]
Ruano, L., Portaccio, E., Goretti, B., Niccolai, C., Severo, M., & Patti, F., et al. (2017). Age and disability drive cognitive impairment in multiple sclerosis across disease subtypes. Multiple Sclerosis 23(9), 1258–1267. [DOI:10.1177/1352458516674367] [PMID]
Sandry, J., Paxton, J., & Sumowski, J. F. (2016). General mathematical ability predicts PASAT performance in MS patients: Implications for clinical interpretation and cognitive reserve. Journal of the International Neuropsychological Society, 22(3), 375–378. [DOI:10.1017/S1355617715001307] [PMID]
Sbardella, E., Upadhyay, N., Tona, F., Prosperini, L., De Giglio, L., & Petsas, N., et al. (2017). Dentate nucleus connectivity in adult patients with multiple sclerosis: Functional changes at rest and correlation with clinical features. Multiple Sclerosis, 23(4), 546–555. [DOI:10.1177/1352458516657438] [PMID]
Schmah, T., Yourganov, G., Zemel, R. S., Hinton, G. E., Small, S. L., & Strother, S. C. (2010). Comparing classification methods for longitudinal fMRI studies. Neural Computation, 22(11), 2729–2762. [DOI:10.1162/NECO_a_00024] [PMID]
Sheng, J., Wang, B., Zhang, Q., Liu, Q., Ma, Y., Liu, W., et al. (2019). A novel joint HCPMMP method for automatically classifying Alzheimer's and different stage MCI patients. Behavioural Brain Research, 365, 210–221. [DOI:10.1016/j.bbr.2019.03.004] [PMID]
Smith S. M. (2002). Fast robust automated brain extraction. Human Brain Mapping, 17(3), 143–155. [DOI:10.1002/hbm.10062] [PMID] [PMCID]
Spiteri, S., Hassa, T., Claros-Salinas, D., Dettmers, C., & Schoenfeld, M. A. (2019). Neural correlates of effort-dependent and effort-independent cognitive fatigue components in patients with multiple sclerosis. Multiple Sclerosis, 25(2), 256–266. [DOI:10.1177/1352458517743090] [PMID]
Tacchino, A., Saiote, C., Brichetto, G., Bommarito, G., Roccatagliata, L., & Cordano, C., et al. (2018). Motor imagery as a function of disease severity in multiple sclerosis: An fMRI Study. Frontiers in Human Neuroscience, 11, 628. [DOI:10.3389/fnhum.2017.00628] [PMID] [PMCID]
Tavazzi, E., Bergsland, N., Cattaneo, D., Gervasoni, E., Laganà, M. M., & Dipasquale, O., et al. (2018). Effects of motor rehabilitation on mobility and brain plasticity in multiple sclerosis: A structural and functional MRI study. Journal of Neurology, 265(6), 1393–1401. [DOI:10.1007/s00415-018-8859-y] [PMID]
Thompson, W. H., & Fransson, P. (2015). The frequency dimension of fMRI dynamic connectivity: Network connectivity, functional hubs and integration in the resting brain. NeuroImage, 121, 227–242. [DOI:10.1016/j.neuroimage.2015.07.022] [PMID]
Tommasin, S., De Giglio, L., Ruggieri, S., Petsas, N., Giannì, C., & Pozzilli, C., et al. (2018). Relation between functional connectivity and disability in multiple sclerosis: A non-linear model. Journal of Neurology, 265(12), 2881–2892. [DOI:10.1007/s00415-018-9075-5] [PMID]
Trapp, B. D., Vignos, M., Dudman, J., Chang, A., Fisher, E., & Staugaitis, S. M., et al. (2018). Cortical neuronal densities and cerebral white matter demyelination in multiple sclerosis: A retrospective study. The Lancet. Neurology, 17(10), 870–884.[DOI:10.1016/S1474-4422(18)30245-X] [PMID] [PMCID]
Vacchi, L., Rocca, M. A., Meani, A., Rodegher, M., Martinelli, V., & Comi, G., et al. (2017). Working memory network dysfunction in relapse-onset multiple sclerosis phenotypes: A clinical-imaging evaluation. Multiple Sclerosis, 23(4), 577–587. [DOI:10.1177/1352458516656809] [PMID]
van Geest, Q., Hulst, H. E., Meijer, K. A., Hoyng, L., Geurts, J. J. G., & Douw, L. (2018). The importance of hippocampal dynamic connectivity in explaining memory function in multiple sclerosis. Brain and Behavior, 8(5), e00954. [DOI:10.1002/brb3.954] [PMID] [PMCID]
Wang, Z., Alahmadi, A., Zhu, D., & Li, T. (2015). Brain functional connectivity analysis using mutual information. Paper presented at the 2015 IEEE Global Conference on Signal and Information Processing. Orlando, FL, USA; 16 December 2015. [DOI:10.1109/GlobalSIP.2015.7418254]
Weier, K., Banwell, B., Cerasa, A., Collins, D. L., Dogonowski, A. M., & Lassmann, H., et al. (2015). The role of the cerebellum in multiple sclerosis. Cerebellum, 14(3), 364–374. [DOI:10.1007/s12311-014-0634-8] [PMID]
Welton, T., Constantinescu, C. S., Auer, D. P., & Dineen, R. A. (2020). Graph theoretic analysis of brain connectomics in multiple sclerosis: Reliability and relationship with cognition. Brain Connectivity, 10(2), 95–104. [DOI:10.1089/brain.2019.0717] [PMID] [PMCID]
Wen, W., Zhu, W., He, Y., Kochan, N. A., Reppermund, S., & Slavin, M. J., et al. (2011). Discrete neuroanatomical networks are associated with specific cognitive abilities in old age. The Journal of Neuroscience, 31(4), 1204–1212. [DOI:10.1523/JNEUROSCI.4085-10.2011] [PMID] [PMCID]
Xia, M., Wang, J., & He, Y. (2013). BrainNet Viewer: A network visualization tool for human brain connectomics. Plos One, 8(7), e68910. [DOI:10.1371/journal.pone.0068910] [PMID] [PMCID]
Yang, Y., Solis-Escalante, T., Yao, J., Daffertshofer, A., Schouten, A. C., & van der Helm, F. C. (2016). A general approach for quantifying nonlinear connectivity in the nervous system based on phase coupling. International Journal of Neural Systems, 26(1), 1550031. [DOI:10.1142/S0129065715500318] [PMID]
Yourganov, G., Schmah, T., Churchill, N. W., Berman, M. G., Grady, C. L., & Strother, S. C. (2014). Pattern classification of fMRI data: Applications for analysis of spatially distributed cortical networks. NeuroImage, 96, 117–132. [DOI:10.1016/j.neuroimage.2014.03.074] [PMID]
Zhao, Y., & Zhang, Y. (2008). Comparison of decision tree methods for finding active objects. Advances in Space Research, 41(12), 1955-1959. [DOI:10.1016/j.asr.2007.07.020]
Zhao, Y., Zhao, Y., Durongbhan, P., Chen, L., Liu, J., & Billings, S. A., et al. (2020). Imaging of nonlinear and dynamic functional brain connectivity based on eeg recordings with the application on the diagnosis of alzheimer's disease. IEEE Transactions on Medical Imaging, 39(5), 1571–1581. [DOI:10.1109/TMI.2019.2953584] [PMID]
Zurita, M., Montalba, C., Labbé, T., Cruz, J. P., Dalboni da Rocha, J., & Tejos, C., et al. (2018). Characterization of relapsing-remitting multiple sclerosis patients using support vector machine classifications of functional and diffusion MRI data. NeuroImage. Clinical, 20, 724–730. [DOI:10.1016/j.nicl.2018.09.002] [PMID] [PMCID]
Type of Study: Original |
Subject:
Computational Neuroscience
Received: 2021/09/2 | Accepted: 2022/01/24 | Published: 2023/11/1
Received: 2021/09/2 | Accepted: 2022/01/24 | Published: 2023/11/1
Send email to the article author
| Rights and permissions | |
 |
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License. |





