Volume 14, Issue 4 (July & August 2023)
BCN 2023, 14(4): 491-500 |
Back to browse issues page
Download citation:
BibTeX | RIS | EndNote | Medlars | ProCite | Reference Manager | RefWorks
Send citation to:



BibTeX | RIS | EndNote | Medlars | ProCite | Reference Manager | RefWorks
Send citation to:
Nahtani M, Siahi M, Razjouyan J. Astrocytic-based Controller Shifts Epileptic Activity to the Chaotic State. BCN 2023; 14 (4) :491-500
URL: http://bcn.iums.ac.ir/article-1-2120-en.html
URL: http://bcn.iums.ac.ir/article-1-2120-en.html
1- Department of Computer and Electrical Science, Faculty of Engineering, Garmsar Branch, Islamic Azad University, Garmsar, Iran.
2- Institute for Clinical & Translational Research (ICTR), Baylor College of Medicine, Houston, The United States of America.
2- Institute for Clinical & Translational Research (ICTR), Baylor College of Medicine, Houston, The United States of America.
Full-Text [PDF 2101 kb]
| Abstract (HTML)
Full-Text:
1. Introduction
Modulating the dynamic properties of neuronal networks (Sarkisian, 2001) using nonlinear techniques is a common method to control seizures (Aihara, 2012; de Paula & Savi, 2008). These methods usually assume a tiny stimulus, applied at an accurate short time, capable of interfering with the dynamics of brain excitability to change the dynamics from a periodic and synchronized activity into a desynchronized neuronal firing (Milton & Jung, 2003). Since the antiepileptic drugs and surgical excision of the seizure focus as the classic controlling methods are ineffective in about one-third of epileptic patients (Tsakalis et al., 2006), electrical therapeutic methods or, in some cases, supplemental treatment to control seizures through modulating the abnormal neuronal activity could be an alternative (Sunderam et al., 2010). The advantage of this method compared with surgery and drugs is that surgery is irreversible and has permanent effects on some parts of the brain, while the stimulation has a transient ameliorating effect on that specific region of the brain. Furthermore, unlike drugs, the variable dosage of stimulation be can be easily applied in every region. However, because of unknown epileptic dynamics, the duration and accuracy of electrical interference are not completely understood. On the other hand, due to the empirical nature of stimulation paradigm calculation, the intervention may initiate a convulsion in some cases (Sarkisian, 2001). In recent studies, due to the high frequency of brain waves during the seizure, researchers studied the background mechanism of this high-frequency signal to use as a therapeutic intervention (Orban et al., 2001). Chaos anti-control is an application method, based on electrical stimulation and system dynamics, for the treatment and reduction of periodic activity of the nervous system (Christini & Collins, 1995). Schiff et al. introduced the concept of anti-control to increase chaos in epilepsy treatment (Schiff et al., 1994).
Due to the unknown equations of the system dynamics, in the case of cerebral seizures, the only available variable is time series. Thus, the methods of nonlinear control systems are used as a model for the establishment of chaos (Schiff et al., 1994). Feedback control is used to prevent the transition from a chaotic desynchronization state to synchronized periodicity in CA3 hippocampal neuronal populations. As asynchrony is one of the chaos properties, the effort was reducing the degree of synchronization between two populations of neurons in the hippocampus of the brain to restore chaos. The disappearance of chaos, as the dominant state of activity in the normal brain, will lead to epileptic convulsions. Therefore, restoring the chaotic state means control of epilepsy attacks. Astrocytes control the composition of the extracellular fluid, electrolyte homeostasis, and neurotransmitter content (Amiri et al., 2010); hence, they regulate the neural synchrony (Fellin et al., 2004; Seiferta et al., 2010). They have the potential to reverse the synchrony of two coupled neurons by manipulation of the synchronization threshold (Amiri et al., 2013). To implement the astrocyte dynamics, Amiri et al. modeled a neuron-astrocyte circuit to alter the pattern of neuronal firing through astrocyte transmission of communication signals (Nazari et al., 2015; Nazari et al., 2014). On the other hand, the failure of astrocytes increases the susceptibility of hypersynchrony and the firing of neurons in regulatory feedback communication (Amiri et al., 2012). Therefore, astrocytes are attractive candidates to be substituted by a controller to control the chaos in the case that two lattice subnetworks are periodically synchronous.
2. Materials and Methods
In this study, an astrocyte-inspired controller (Amiri et al., 2011) was used to apply a stimulus to two reticular subnetworks of the CA3 region developed due to an epilepsy model. This research focused on the spatiotemporal behavior of the coupled model of a network, in which each node or cell of the network is described by an ordinary differential equation model. The presented network describes the microscopic and spatiotemporal behavior of a small region of the hippocampus. Dynamical behavior of this subnetwork, described by the differential equations, is based on the two-variable model of Hodgkin–Huxley. These equations were originally introduced by Morris and Lecare (M&L) (Morris & Lecar, 1981) as a model of Barnacle muscle fiber; however, they were introduced as a tool to model the pyramidal cell functions in a specified network (Figure 1).
Modulating the dynamic properties of neuronal networks (Sarkisian, 2001) using nonlinear techniques is a common method to control seizures (Aihara, 2012; de Paula & Savi, 2008). These methods usually assume a tiny stimulus, applied at an accurate short time, capable of interfering with the dynamics of brain excitability to change the dynamics from a periodic and synchronized activity into a desynchronized neuronal firing (Milton & Jung, 2003). Since the antiepileptic drugs and surgical excision of the seizure focus as the classic controlling methods are ineffective in about one-third of epileptic patients (Tsakalis et al., 2006), electrical therapeutic methods or, in some cases, supplemental treatment to control seizures through modulating the abnormal neuronal activity could be an alternative (Sunderam et al., 2010). The advantage of this method compared with surgery and drugs is that surgery is irreversible and has permanent effects on some parts of the brain, while the stimulation has a transient ameliorating effect on that specific region of the brain. Furthermore, unlike drugs, the variable dosage of stimulation be can be easily applied in every region. However, because of unknown epileptic dynamics, the duration and accuracy of electrical interference are not completely understood. On the other hand, due to the empirical nature of stimulation paradigm calculation, the intervention may initiate a convulsion in some cases (Sarkisian, 2001). In recent studies, due to the high frequency of brain waves during the seizure, researchers studied the background mechanism of this high-frequency signal to use as a therapeutic intervention (Orban et al., 2001). Chaos anti-control is an application method, based on electrical stimulation and system dynamics, for the treatment and reduction of periodic activity of the nervous system (Christini & Collins, 1995). Schiff et al. introduced the concept of anti-control to increase chaos in epilepsy treatment (Schiff et al., 1994).
Due to the unknown equations of the system dynamics, in the case of cerebral seizures, the only available variable is time series. Thus, the methods of nonlinear control systems are used as a model for the establishment of chaos (Schiff et al., 1994). Feedback control is used to prevent the transition from a chaotic desynchronization state to synchronized periodicity in CA3 hippocampal neuronal populations. As asynchrony is one of the chaos properties, the effort was reducing the degree of synchronization between two populations of neurons in the hippocampus of the brain to restore chaos. The disappearance of chaos, as the dominant state of activity in the normal brain, will lead to epileptic convulsions. Therefore, restoring the chaotic state means control of epilepsy attacks. Astrocytes control the composition of the extracellular fluid, electrolyte homeostasis, and neurotransmitter content (Amiri et al., 2010); hence, they regulate the neural synchrony (Fellin et al., 2004; Seiferta et al., 2010). They have the potential to reverse the synchrony of two coupled neurons by manipulation of the synchronization threshold (Amiri et al., 2013). To implement the astrocyte dynamics, Amiri et al. modeled a neuron-astrocyte circuit to alter the pattern of neuronal firing through astrocyte transmission of communication signals (Nazari et al., 2015; Nazari et al., 2014). On the other hand, the failure of astrocytes increases the susceptibility of hypersynchrony and the firing of neurons in regulatory feedback communication (Amiri et al., 2012). Therefore, astrocytes are attractive candidates to be substituted by a controller to control the chaos in the case that two lattice subnetworks are periodically synchronous.
2. Materials and Methods
In this study, an astrocyte-inspired controller (Amiri et al., 2011) was used to apply a stimulus to two reticular subnetworks of the CA3 region developed due to an epilepsy model. This research focused on the spatiotemporal behavior of the coupled model of a network, in which each node or cell of the network is described by an ordinary differential equation model. The presented network describes the microscopic and spatiotemporal behavior of a small region of the hippocampus. Dynamical behavior of this subnetwork, described by the differential equations, is based on the two-variable model of Hodgkin–Huxley. These equations were originally introduced by Morris and Lecare (M&L) (Morris & Lecar, 1981) as a model of Barnacle muscle fiber; however, they were introduced as a tool to model the pyramidal cell functions in a specified network (Figure 1).
Then, Larter et al. added an equation to M&L equations to replicate the effect of a population of inhibitory interneurons synapsing onto principle pyramidal cells (Larter et al., 1999).
The nonlinear differential equations (Equations 1-3) that describe this model are as follows:

.jpg)
The M&L model consists of Equations 1 and 2 without the αinhZi term of Equation 1. The first and third variables Vi and Zi, are the membrane potentials of the pyramidal and inhibitory cells, respectively, while the second variable, Wi, is the fraction of open potassium channels in the pyramidal cell populations of the mentioned subnetwork. The three variables were applied to node “i” in the lattice. The parameters gca, gK, and gL are the total conductance for the Ca, K, and leakage channels, respectively. VK is the Nernst potential for potassium, which will be used to link neuronal populations and form a lattice (Larter et al., 1999; Raiesdana & Goplayegani, 2013). I indicates the applied current, while ϕ and b are temperature scaling factors. The parameter C in Equation 3 is the differential modifier of the current input to the inhibitory interneuron (Raiesdana & Goplayegani, 2013). Parameters of the simulations are summarized in Appendix A.


By describing three-dimensional ordinary differential equations (ODEs), this model can be an effective control system that satisfies the control resources Such a system is so dynamic that covers different behaviors, such as simple limit cycles, complex periodic oscillations, and chaotic behaviors (Figure 2).
.jpg)
Because this lattice model can delineate the effects of disinhibition on the model dynamics, this work was done to show how the system’s behavior could be altered due to an inhibitory parameter change.
The dynamics of the model
In this part, the dynamic properties of the introduced system were analyzed. The dynamics of nonlinear systems are mostly illustrated by some graphical tools. The effect of inhibition variation on the dynamic behavior of neural networks in the CA3 region was shown in the below diagrams of time series and phase portraits (Figure 2).
It is illustrated in Figure 2a and Figure 2b, system behaviors were altered by changing the parameters of excitation and inhibition and shifted from a chaotic state in part a to a periodic state in part b. The values were selected from Appendix A (Larter et al., 1999), except the amount of V6, b, and C, which were chosen from the research by Nadar et al. (Nadar & Rai, 2012).
Astrocyte-based controller
In this part, the astrocyte function and the astrocyte-based controller were explained.
The astrocyte model
Biological research has confirmed that glial cells function actively in neuronal electrical signaling and information processing (Fellin et al., 2004; Halassa & Haydon, 2010). While astrocytes do not develop electrical activity, they act in response to changes in intracellular calcium concentration (Rosenblum & Pikovsky, 2004). An increase in astrocytic intracellular calcium levels induces the release of glutamate, and changes ATP/ADP ratio, thereby affecting nearby synapses and neurons by a feedback mechanism. Astrocytes make synapse-like contacts individually and in a network with pyramidal and inhibitory neurons (Amiri et al., 2010).
The main cellular mechanism underlying tripartite synapses is as follows: Presynaptic neurons release glutamate as a neurotransmitter following its axon terminal depolarization, and then the released glutamate is bound to its receptor on the astrocyte as well as postsynaptic membrane. Ligand-receptor interaction triggers a series of signal transduction molecules, such as IP3 and DAG, which IP3, in turn, induces calcium release from intracellular stores. This concentration change of Ca2+ originated from the endoplasmic reticulum (ER) source, initiates a calcium wave in astrocytic ensemble via gap junctions, and finally induces the release of gliotransmitters (glutamate and ATP) and regulates the pre- to post-synaptic transmission (Fellin et al., 2004; Halassa & Haydon, 2010). A simple and general mathematical model based on the presented equations and signal transmission through the tripartite synapse including pre- and post-synaptic neurons and astrocytes was introduced by Amiri et al., which is capable of synchronizing two synchronized coupled neural oscillators (Amiri et al., 2012; Amiri et al., 2013; Amiri et al., 2011; Postnov et al., 2009).
The proposed model for the mathematical structure of the controller is as follows (Equations 4-6):
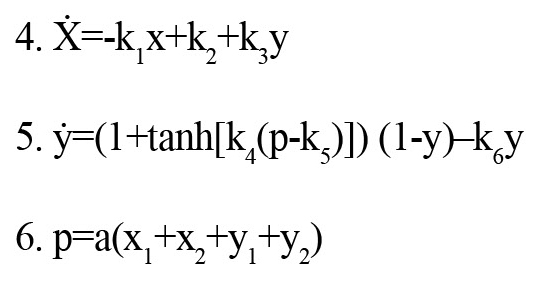
The input p triggers the changes, which then affects the dynamics by the term k3y. The controller output considered and k5 as the threshold parameter used for the activation and inactivation of the controller. The parameters x1, x2, y1, and y2 are controller input signals received from the neural network. The parameter “a” is input gain. The parameters k1-k5 and a are summarized in Appendix B.

Closed-loop dynamics
The controller was applied to two subnetworks lattices of the hexagonal neural system, with each subnetwork affected by the controller output via γX. A schematic illustration of the closed-loop system is shown in Figure 3 (Equations 7, 8).
.jpg)
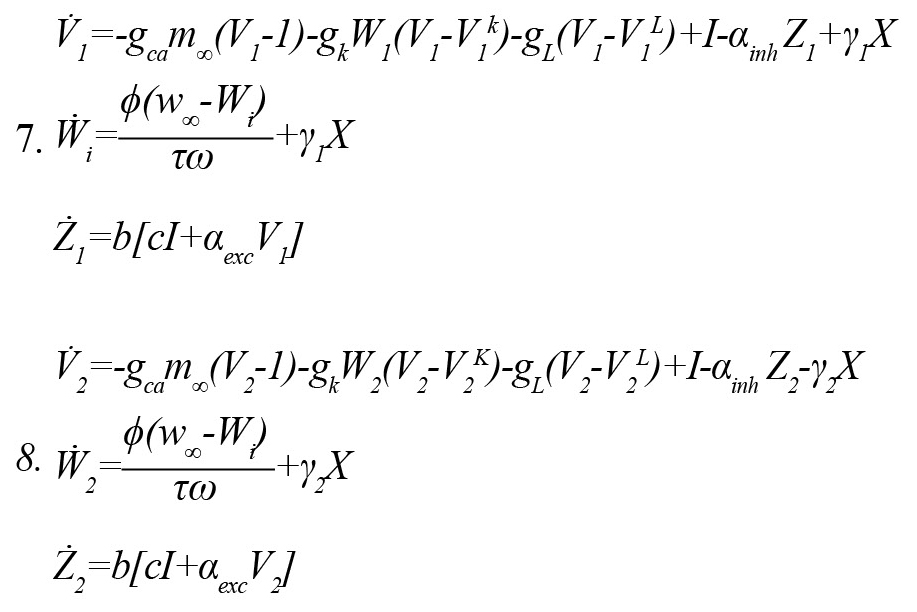
“X" is the control signal, which was applied to the closed-loop system capable of desynchronizing the two lattice subnetworks through the terms γ1X and -γ2X. A positive sign means excitation and a negative sign means inhibition. Input p was considered as p=a(V1+V2+W1+ W2), an observer that detects the instantaneous change in the membrane potential of the pyramidal neurons and K+ channels in the two subnetworks and then applies proper controlling signal. Consequently, the closed-loop system was protected from a transition to periodicity.
4. Results
Initial values (C=0.13, V6=0.6, and b=0.1) were employed to run the model and a low-dimensional chaotic behavior resulted, subsequently. This low level of inhibition leads to a reduced agitated state and the onset of an epileptic seizure (Nadar & Rai, 2012). It is well known that the seizure state (in its pathologic form) precedes the seizure appearance and a gradual development of the seizure dominance will be pursued. Therefore, it seems that this is a proper phase to apply controlling stimulation (Raiesdana & Goplayegani, 2013). This phase is shown in Figure 4.
.jpg)
According to Section II. A, initially, we kept the model of low-dimensional chaotic behavior (the simulated state shown in Figure 4, pre-seizure state). The controller was turned on in this state, without any manipulating the parameter values. As it is illustrated in Figure 5, the neural model behavior returned to the chaotic state. The parametric values of the closed-loop system are summarized in Appendix B. Results showed that (controller output) has a strengthening effect on inhibitory cells.
.jpg)
5. Discussion
This research aimed to evaluate the effect of an astrocyte-based mathematical model output onto two CA3 synchronized subnetworks as a convulsion model. The results demonstrated that synchronization was desynchronized and the network was returned to its pre-epileptic chaotic behavior with little effort of astrocyte-based controller to maintain the chaotic state.
This study focused on the influence of the astrocyte-based controller on two subnetworks of the lattice model of hippocampal CA3 neurons. Upon the mathematical resolving and simulation findings, the controller has the potential to break apart the periodicity in the epileptic model. It seems that a feedback controller can be a reliable choice to control this model because of its nonlinear characteristics. It can process the amount of lattice networks’ output and then apply the controller output to lattice sub-networks. Thus, the network is observed every time, and the controller can intervene every time it is needed.
By changing the dynamic characteristics of epilepsy by applying external electrical stimulation, it seems that there are some confounding factors for a closed-loop control scheme. The results showed that by using a biologically plausible controller, the epileptic periodicity will be resolved. It is well documented that healthy astrocytes will help the network milieu to be cleared of any excitability agent, such as glutamate, which may further provoke another oscillatory activity. Furthermore, as our results showed, the output of the astrocytic model, similar to chemical messengers, such as gliotransmitters, may turn down the tuning knob of periodicity. This notion may be helpful regarding the result of a study by Rogawski et al. indicating that the population of astrocytes increases in the early phases of epileptogenesis, which makes the epileptic subnetwork a good candidate for the application of the astrocytic-based model (Rogawski, 2005). On the other hand, Bedner et al. showed a decrease in the number of gap junctions between astrocytes, as key elements of astrocytic synchrony to react to any change of network conditions in the initial establishment phases of epileptogenesis (Bedner et al., 2015). This type of astrocyte susceptibility to pathologic insult demonstrates the rationale behind the inability of endogenous astrocytic function in healing or cessation of epileptogenic development. Therefore, it is suggested that the replacement of epileptic-incapacitated astrocytes with an astrocyte-based controller could help prevent the transition to periodic or even reversion of the seizure state to disordered conditions. The effectiveness of the model may be related to the direct effects on the neuronal functions and/or activating the regulatory function of remaining healthy astrocytes (Amiri et al., 2013).
Additionally, simulating the time series of the lattice model showed that the natural complex behavior of the brain will be dominated after restoring the chaotic state. The use of this controller to model noisy synchronized epileptic states is instructive for future work, as they seem to be more biologically plausible. Furthermore, investigation of this model may be useful in the periodic non-synchronized epileptic state, which is a determinant of status epilepticus and other nonstop seizure attacks.
Ethical Considerations
Compliance with ethical guidelines
There were no ethical considerations to be considered in this research.
Funding
This research was extracted from thesis of Mojde Nahtani, approved by the Islamic Azad University, Garmsar Branch.
Authors' contributions
Conceptualization and supervision: Mahdi Siahi; Methodology: Javad Razjouyan; Investigation, data analysis and writing the manuscript: Mojde Nahtani.
Conflict of interest
The authors declared no conflict of interest.
Acknowledgments
The authors would like to thank Raima Larter, professor of chemistry, previously at the Department of Chemistry, Indiana University, for her worthy help and Sreenivasan Rajamoni Nader, National Institute of mental health Bethesda, USA. for his precious instructions.
References
Aihara, K. (2012). Chaos and its applications. Procedia IUTAM, 5, 199-203. [DOI:10.1016/j.piutam.2012.06.027]
Amiri, M., Bahrami, F., & Janahmadi, M. (2010). Functional modeling of astrocytes in epilepsy: A feedback system perspective. Neural Computing and Applications, 20, 1131-1139. [Link]
Amiri, M., Hosseinmardi, N., Bahrami, F., & Janahmadi, M. (2013). Astrocyte- neuron interaction as a mechanism responsible for generation of neural synchrony: A study based on modeling and experiments. Journal of Computational Neuroscience, 34(3), 489–504. [DOI:10.1007/s10827-012-0432-6] [PMID]
Amiri, M., Montaseri, G., & Bahrami, F. (2011). On the role of astrocytes in synchronization of two coupled neurons: A mathematical perspective. Biological Cybernetics, 105(2), 153–166.[DOI:10.1007/s00422-011-0455-5] [PMID]
Bedner, P., Dupper, A., Hüttmann, K., Müller, J., Herde, M. K., & Dublin, P., et al. (2015). Astrocyte uncoupling as a cause of human temporal lobe epilepsy. Brain, 138(Pt 5), 1208-1222. [DOI:10.1093/brain/awv067] [PMID]
Christini, D. J., & Collins, J. J. (1995). Controlling nonchaotic neuronal noise using chaos control techniques. Physical Review Letters, 75(14), 2782–2785.[DOI:10.1103/PhysRevLett.75.2782] [PMID]
De Paula, A. S., & Savi, M. A. (2008). A multiparameter, chaos control method applied to maps. Brazilian Journal of Physics, 38(4), 536-542. [DOI:10.1590/S0103-97332008000500002]
Fellin, T., Pascual, O., Gobbo, S., Pozzan, T., Haydon, P. G., & Carmignoto, G. (2004). Neuronal synchrony mediated by astrocytic glutamate through activation of extrasynaptic NMDA receptors. Neuron, 43(5), 729–743. [DOI:10.1016/j.neuron.2004.08.011] [PMID]
Halassa, M. M., & Haydon, P. G. (2010). Integrated brain circuits: Astrocytic networks modulate neuronal activity and behavior. Annual Review of Physiology, 72, 335-355. [DOI:10.1146/annurev-physiol-021909-135843] [PMID]
Larter, R., Speelman, B., & Worth, R. M. (1999). A coupled ordinary differential equation lattice model for the simulation of epileptic seizures. Chaos, 9(3), 795-804. [DOI:10.1063/1.166453] [PMID]
Milton, J., & Jung, P. (2003). Epilepsy as a dynamic disease. Berlin: Springer. [Link]
Morris, C., & Lecar, H. (1981). Voltage oscillationsin the barnaclegiant muscle fiber. Biophysical Journal, 35(1), 193-213. [DOI:10.1016/S0006-3495(81)84782-0] [PMID]
Nadar, S. R., & Rai, V. (2012). Transient periodicity in a morris-lecar neural system. International Scholarly Research Notices, 2012, 1-7. [DOI:10.5402/2012/546315]
Nazari, S., Faez, K., Amiri, M., & Karami, E. (2015). A digital implementation of neuron-astrocyte interaction for neuromorphic applications. Neural networks: The Official Journal of the International Neural Network Society, 66, 79–90. [DOI:10.1016/j.neunet.2015.01.005] [PMID]
Nazari, S., Faez, K., Karami, E., & Amiri, M. (2014). A digital neurmorphic circuit for a simplified model of astrocyte dynamics. Neuroscience Letters, 582, 21–26. [DOI:10.1016/j.neulet.2014.07.055] [PMID]
Orbán, G., Kiss, T., Lengyel, M., & Erdi, P. (2001). Hippocampal rhythm generation: Gamma-related theta-frequency resonance in CA3 interneurons. Biological Cybernetics, 84(2), 123–132.[DOI:10.1007/s004220000199] [PMID]
Postnov, D. E., Koreshkov, R. N., Brazhe, N. A., Brazhe, A. R., & Sosnovtseva, O. V. (2009). Dynamical patterns of calcium signaling in a functional model of neuron-astrocyte networks. J Biol Phys, 35(4), 425-445. [DOI:10.1007/s10867-009-9156-x] [PMID]
Raiesdana, S., & Goplayegani, S. M. H. (2013). Study on chaos anti-control for hippocampal models of epilepsy. Neurocomputing, 111, 54-69. [DOI:10.1016/j.neucom.2012.11.033]
Rogawski, M. A. (2005). Astrocytes get in the act in epilepsy. Nature Medicine, 11(9), 919-920. [DOI:10.1038/nm0905-919] [PMID]
Rosenblum, M. G., & Pikovsky, A. S. (2004). Controlling synchronization in an ensembles of globally coupled oscillators. Physical Review Letters, 92(11), 114102. [DOI:10.1103/PhysRevLett.92.114102] [PMID]
Sarkisian, M. R. (2001). Overview of the current animal models for human seizure and epileptic disorders. Epilepsy & Behavior, 2(3), 201-216. [DOI:10.1006/ebeh.2001.0193] [PMID]
Schiff, S. J., Jerger, K., Duong, D. H., Chang, T., Spano, M. L., & Ditto, W. L. (1994). Controlling chaos in the brain. Nature, 370(6491), 615-620. [DOI:10.1038/370615a0] [PMID]
Seiferta, G., Carmignotob, G., & Steinhäusera, C. (2010). Astrocyte dysfunction in epilepsy. Brain Research Reviews, 63(1-2), 212–221. [DOI:10.1016/j.brainresrev.2009.10.004] [PMID]
Sunderam, S., Gluckman, B., Reato, D., & Bikson, M. (2010). Toward rational design of electrical stimulation strategies for epilepsy control. Epilepsy & Behavior: E&B, 17(1), 6–22. [DOI:10.1016/j.yebeh.2009.10.017] [PMID]
Tsakalis, K., Chakravarthy, N., Sabesan, s., & Iasemidis, L. D. (2006). A feedback control system view of epileptic seizure. Cybern Syst Anal 42, 483–495. [DOI: 10.1007/s10559-006-0087-2]
The nonlinear differential equations (Equations 1-3) that describe this model are as follows:

.jpg)
The M&L model consists of Equations 1 and 2 without the αinhZi term of Equation 1. The first and third variables Vi and Zi, are the membrane potentials of the pyramidal and inhibitory cells, respectively, while the second variable, Wi, is the fraction of open potassium channels in the pyramidal cell populations of the mentioned subnetwork. The three variables were applied to node “i” in the lattice. The parameters gca, gK, and gL are the total conductance for the Ca, K, and leakage channels, respectively. VK is the Nernst potential for potassium, which will be used to link neuronal populations and form a lattice (Larter et al., 1999; Raiesdana & Goplayegani, 2013). I indicates the applied current, while ϕ and b are temperature scaling factors. The parameter C in Equation 3 is the differential modifier of the current input to the inhibitory interneuron (Raiesdana & Goplayegani, 2013). Parameters of the simulations are summarized in Appendix A.


By describing three-dimensional ordinary differential equations (ODEs), this model can be an effective control system that satisfies the control resources Such a system is so dynamic that covers different behaviors, such as simple limit cycles, complex periodic oscillations, and chaotic behaviors (Figure 2).
.jpg)
Because this lattice model can delineate the effects of disinhibition on the model dynamics, this work was done to show how the system’s behavior could be altered due to an inhibitory parameter change.
The dynamics of the model
In this part, the dynamic properties of the introduced system were analyzed. The dynamics of nonlinear systems are mostly illustrated by some graphical tools. The effect of inhibition variation on the dynamic behavior of neural networks in the CA3 region was shown in the below diagrams of time series and phase portraits (Figure 2).
It is illustrated in Figure 2a and Figure 2b, system behaviors were altered by changing the parameters of excitation and inhibition and shifted from a chaotic state in part a to a periodic state in part b. The values were selected from Appendix A (Larter et al., 1999), except the amount of V6, b, and C, which were chosen from the research by Nadar et al. (Nadar & Rai, 2012).
Astrocyte-based controller
In this part, the astrocyte function and the astrocyte-based controller were explained.
The astrocyte model
Biological research has confirmed that glial cells function actively in neuronal electrical signaling and information processing (Fellin et al., 2004; Halassa & Haydon, 2010). While astrocytes do not develop electrical activity, they act in response to changes in intracellular calcium concentration (Rosenblum & Pikovsky, 2004). An increase in astrocytic intracellular calcium levels induces the release of glutamate, and changes ATP/ADP ratio, thereby affecting nearby synapses and neurons by a feedback mechanism. Astrocytes make synapse-like contacts individually and in a network with pyramidal and inhibitory neurons (Amiri et al., 2010).
The main cellular mechanism underlying tripartite synapses is as follows: Presynaptic neurons release glutamate as a neurotransmitter following its axon terminal depolarization, and then the released glutamate is bound to its receptor on the astrocyte as well as postsynaptic membrane. Ligand-receptor interaction triggers a series of signal transduction molecules, such as IP3 and DAG, which IP3, in turn, induces calcium release from intracellular stores. This concentration change of Ca2+ originated from the endoplasmic reticulum (ER) source, initiates a calcium wave in astrocytic ensemble via gap junctions, and finally induces the release of gliotransmitters (glutamate and ATP) and regulates the pre- to post-synaptic transmission (Fellin et al., 2004; Halassa & Haydon, 2010). A simple and general mathematical model based on the presented equations and signal transmission through the tripartite synapse including pre- and post-synaptic neurons and astrocytes was introduced by Amiri et al., which is capable of synchronizing two synchronized coupled neural oscillators (Amiri et al., 2012; Amiri et al., 2013; Amiri et al., 2011; Postnov et al., 2009).
The proposed model for the mathematical structure of the controller is as follows (Equations 4-6):
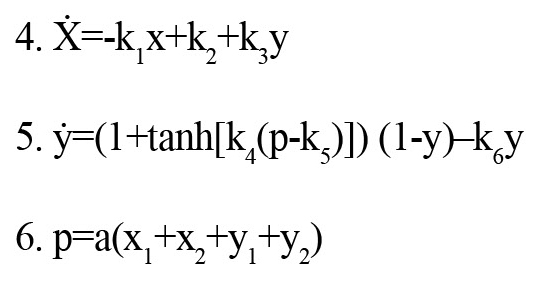
The input p triggers the changes, which then affects the dynamics by the term k3y. The controller output considered and k5 as the threshold parameter used for the activation and inactivation of the controller. The parameters x1, x2, y1, and y2 are controller input signals received from the neural network. The parameter “a” is input gain. The parameters k1-k5 and a are summarized in Appendix B.

Closed-loop dynamics
The controller was applied to two subnetworks lattices of the hexagonal neural system, with each subnetwork affected by the controller output via γX. A schematic illustration of the closed-loop system is shown in Figure 3 (Equations 7, 8).
.jpg)
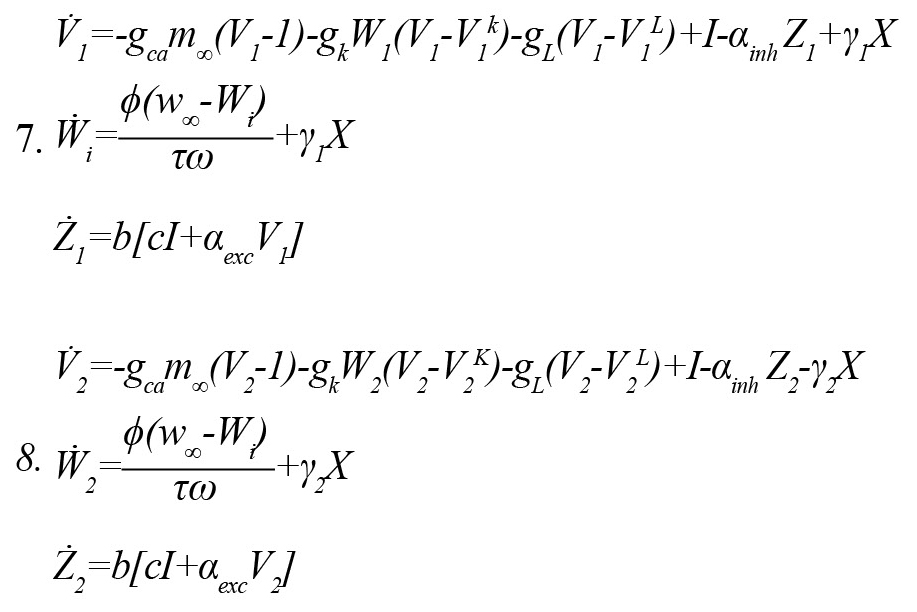
“X" is the control signal, which was applied to the closed-loop system capable of desynchronizing the two lattice subnetworks through the terms γ1X and -γ2X. A positive sign means excitation and a negative sign means inhibition. Input p was considered as p=a(V1+V2+W1+ W2), an observer that detects the instantaneous change in the membrane potential of the pyramidal neurons and K+ channels in the two subnetworks and then applies proper controlling signal. Consequently, the closed-loop system was protected from a transition to periodicity.
4. Results
Initial values (C=0.13, V6=0.6, and b=0.1) were employed to run the model and a low-dimensional chaotic behavior resulted, subsequently. This low level of inhibition leads to a reduced agitated state and the onset of an epileptic seizure (Nadar & Rai, 2012). It is well known that the seizure state (in its pathologic form) precedes the seizure appearance and a gradual development of the seizure dominance will be pursued. Therefore, it seems that this is a proper phase to apply controlling stimulation (Raiesdana & Goplayegani, 2013). This phase is shown in Figure 4.
.jpg)
According to Section II. A, initially, we kept the model of low-dimensional chaotic behavior (the simulated state shown in Figure 4, pre-seizure state). The controller was turned on in this state, without any manipulating the parameter values. As it is illustrated in Figure 5, the neural model behavior returned to the chaotic state. The parametric values of the closed-loop system are summarized in Appendix B. Results showed that (controller output) has a strengthening effect on inhibitory cells.
.jpg)
5. Discussion
This research aimed to evaluate the effect of an astrocyte-based mathematical model output onto two CA3 synchronized subnetworks as a convulsion model. The results demonstrated that synchronization was desynchronized and the network was returned to its pre-epileptic chaotic behavior with little effort of astrocyte-based controller to maintain the chaotic state.
This study focused on the influence of the astrocyte-based controller on two subnetworks of the lattice model of hippocampal CA3 neurons. Upon the mathematical resolving and simulation findings, the controller has the potential to break apart the periodicity in the epileptic model. It seems that a feedback controller can be a reliable choice to control this model because of its nonlinear characteristics. It can process the amount of lattice networks’ output and then apply the controller output to lattice sub-networks. Thus, the network is observed every time, and the controller can intervene every time it is needed.
By changing the dynamic characteristics of epilepsy by applying external electrical stimulation, it seems that there are some confounding factors for a closed-loop control scheme. The results showed that by using a biologically plausible controller, the epileptic periodicity will be resolved. It is well documented that healthy astrocytes will help the network milieu to be cleared of any excitability agent, such as glutamate, which may further provoke another oscillatory activity. Furthermore, as our results showed, the output of the astrocytic model, similar to chemical messengers, such as gliotransmitters, may turn down the tuning knob of periodicity. This notion may be helpful regarding the result of a study by Rogawski et al. indicating that the population of astrocytes increases in the early phases of epileptogenesis, which makes the epileptic subnetwork a good candidate for the application of the astrocytic-based model (Rogawski, 2005). On the other hand, Bedner et al. showed a decrease in the number of gap junctions between astrocytes, as key elements of astrocytic synchrony to react to any change of network conditions in the initial establishment phases of epileptogenesis (Bedner et al., 2015). This type of astrocyte susceptibility to pathologic insult demonstrates the rationale behind the inability of endogenous astrocytic function in healing or cessation of epileptogenic development. Therefore, it is suggested that the replacement of epileptic-incapacitated astrocytes with an astrocyte-based controller could help prevent the transition to periodic or even reversion of the seizure state to disordered conditions. The effectiveness of the model may be related to the direct effects on the neuronal functions and/or activating the regulatory function of remaining healthy astrocytes (Amiri et al., 2013).
Additionally, simulating the time series of the lattice model showed that the natural complex behavior of the brain will be dominated after restoring the chaotic state. The use of this controller to model noisy synchronized epileptic states is instructive for future work, as they seem to be more biologically plausible. Furthermore, investigation of this model may be useful in the periodic non-synchronized epileptic state, which is a determinant of status epilepticus and other nonstop seizure attacks.
Ethical Considerations
Compliance with ethical guidelines
There were no ethical considerations to be considered in this research.
Funding
This research was extracted from thesis of Mojde Nahtani, approved by the Islamic Azad University, Garmsar Branch.
Authors' contributions
Conceptualization and supervision: Mahdi Siahi; Methodology: Javad Razjouyan; Investigation, data analysis and writing the manuscript: Mojde Nahtani.
Conflict of interest
The authors declared no conflict of interest.
Acknowledgments
The authors would like to thank Raima Larter, professor of chemistry, previously at the Department of Chemistry, Indiana University, for her worthy help and Sreenivasan Rajamoni Nader, National Institute of mental health Bethesda, USA. for his precious instructions.
References
Aihara, K. (2012). Chaos and its applications. Procedia IUTAM, 5, 199-203. [DOI:10.1016/j.piutam.2012.06.027]
Amiri, M., Bahrami, F., & Janahmadi, M. (2010). Functional modeling of astrocytes in epilepsy: A feedback system perspective. Neural Computing and Applications, 20, 1131-1139. [Link]
Amiri, M., Hosseinmardi, N., Bahrami, F., & Janahmadi, M. (2013). Astrocyte- neuron interaction as a mechanism responsible for generation of neural synchrony: A study based on modeling and experiments. Journal of Computational Neuroscience, 34(3), 489–504. [DOI:10.1007/s10827-012-0432-6] [PMID]
Amiri, M., Montaseri, G., & Bahrami, F. (2011). On the role of astrocytes in synchronization of two coupled neurons: A mathematical perspective. Biological Cybernetics, 105(2), 153–166.[DOI:10.1007/s00422-011-0455-5] [PMID]
Bedner, P., Dupper, A., Hüttmann, K., Müller, J., Herde, M. K., & Dublin, P., et al. (2015). Astrocyte uncoupling as a cause of human temporal lobe epilepsy. Brain, 138(Pt 5), 1208-1222. [DOI:10.1093/brain/awv067] [PMID]
Christini, D. J., & Collins, J. J. (1995). Controlling nonchaotic neuronal noise using chaos control techniques. Physical Review Letters, 75(14), 2782–2785.[DOI:10.1103/PhysRevLett.75.2782] [PMID]
De Paula, A. S., & Savi, M. A. (2008). A multiparameter, chaos control method applied to maps. Brazilian Journal of Physics, 38(4), 536-542. [DOI:10.1590/S0103-97332008000500002]
Fellin, T., Pascual, O., Gobbo, S., Pozzan, T., Haydon, P. G., & Carmignoto, G. (2004). Neuronal synchrony mediated by astrocytic glutamate through activation of extrasynaptic NMDA receptors. Neuron, 43(5), 729–743. [DOI:10.1016/j.neuron.2004.08.011] [PMID]
Halassa, M. M., & Haydon, P. G. (2010). Integrated brain circuits: Astrocytic networks modulate neuronal activity and behavior. Annual Review of Physiology, 72, 335-355. [DOI:10.1146/annurev-physiol-021909-135843] [PMID]
Larter, R., Speelman, B., & Worth, R. M. (1999). A coupled ordinary differential equation lattice model for the simulation of epileptic seizures. Chaos, 9(3), 795-804. [DOI:10.1063/1.166453] [PMID]
Milton, J., & Jung, P. (2003). Epilepsy as a dynamic disease. Berlin: Springer. [Link]
Morris, C., & Lecar, H. (1981). Voltage oscillationsin the barnaclegiant muscle fiber. Biophysical Journal, 35(1), 193-213. [DOI:10.1016/S0006-3495(81)84782-0] [PMID]
Nadar, S. R., & Rai, V. (2012). Transient periodicity in a morris-lecar neural system. International Scholarly Research Notices, 2012, 1-7. [DOI:10.5402/2012/546315]
Nazari, S., Faez, K., Amiri, M., & Karami, E. (2015). A digital implementation of neuron-astrocyte interaction for neuromorphic applications. Neural networks: The Official Journal of the International Neural Network Society, 66, 79–90. [DOI:10.1016/j.neunet.2015.01.005] [PMID]
Nazari, S., Faez, K., Karami, E., & Amiri, M. (2014). A digital neurmorphic circuit for a simplified model of astrocyte dynamics. Neuroscience Letters, 582, 21–26. [DOI:10.1016/j.neulet.2014.07.055] [PMID]
Orbán, G., Kiss, T., Lengyel, M., & Erdi, P. (2001). Hippocampal rhythm generation: Gamma-related theta-frequency resonance in CA3 interneurons. Biological Cybernetics, 84(2), 123–132.[DOI:10.1007/s004220000199] [PMID]
Postnov, D. E., Koreshkov, R. N., Brazhe, N. A., Brazhe, A. R., & Sosnovtseva, O. V. (2009). Dynamical patterns of calcium signaling in a functional model of neuron-astrocyte networks. J Biol Phys, 35(4), 425-445. [DOI:10.1007/s10867-009-9156-x] [PMID]
Raiesdana, S., & Goplayegani, S. M. H. (2013). Study on chaos anti-control for hippocampal models of epilepsy. Neurocomputing, 111, 54-69. [DOI:10.1016/j.neucom.2012.11.033]
Rogawski, M. A. (2005). Astrocytes get in the act in epilepsy. Nature Medicine, 11(9), 919-920. [DOI:10.1038/nm0905-919] [PMID]
Rosenblum, M. G., & Pikovsky, A. S. (2004). Controlling synchronization in an ensembles of globally coupled oscillators. Physical Review Letters, 92(11), 114102. [DOI:10.1103/PhysRevLett.92.114102] [PMID]
Sarkisian, M. R. (2001). Overview of the current animal models for human seizure and epileptic disorders. Epilepsy & Behavior, 2(3), 201-216. [DOI:10.1006/ebeh.2001.0193] [PMID]
Schiff, S. J., Jerger, K., Duong, D. H., Chang, T., Spano, M. L., & Ditto, W. L. (1994). Controlling chaos in the brain. Nature, 370(6491), 615-620. [DOI:10.1038/370615a0] [PMID]
Seiferta, G., Carmignotob, G., & Steinhäusera, C. (2010). Astrocyte dysfunction in epilepsy. Brain Research Reviews, 63(1-2), 212–221. [DOI:10.1016/j.brainresrev.2009.10.004] [PMID]
Sunderam, S., Gluckman, B., Reato, D., & Bikson, M. (2010). Toward rational design of electrical stimulation strategies for epilepsy control. Epilepsy & Behavior: E&B, 17(1), 6–22. [DOI:10.1016/j.yebeh.2009.10.017] [PMID]
Tsakalis, K., Chakravarthy, N., Sabesan, s., & Iasemidis, L. D. (2006). A feedback control system view of epileptic seizure. Cybern Syst Anal 42, 483–495. [DOI: 10.1007/s10559-006-0087-2]
Type of Study: Original |
Subject:
Computational Neuroscience
Received: 2020/03/9 | Accepted: 2021/05/23 | Published: 2023/07/1
Received: 2020/03/9 | Accepted: 2021/05/23 | Published: 2023/07/1
Send email to the article author
| Rights and permissions | |
 |
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License. |








.jpg)
