Volume 8, Issue 5 (September & October 2017)
BCN 2017, 8(5): 371-386 |
Back to browse issues page
Download citation:
BibTeX | RIS | EndNote | Medlars | ProCite | Reference Manager | RefWorks
Send citation to:



BibTeX | RIS | EndNote | Medlars | ProCite | Reference Manager | RefWorks
Send citation to:
Siyah Mansoory M, Oghabian M A, Jafari A H, Shahbabaie A. Analysis of Resting-State fMRI Topological Graph Theory Properties in Methamphetamine Drug Users Applying Box-Counting Fractal Dimension. BCN 2017; 8 (5) :371-386
URL: http://bcn.iums.ac.ir/article-1-741-en.html
URL: http://bcn.iums.ac.ir/article-1-741-en.html
1- Department of Medical Physics & Biomedical Engineering, School of Medicine, Tehran University of Medical Sciences, Tehran, Iran.
2- Department of Neuro-Imaging and Analysis, Research Center for Molecular and Cellular Imaging, Tehran University of Medical Sciences, Tehran, Iran
2- Department of Neuro-Imaging and Analysis, Research Center for Molecular and Cellular Imaging, Tehran University of Medical Sciences, Tehran, Iran
Keywords: Graph theory, Box-counting fractal dimension, Mutual information, Linear correlation, Methamphetamine
Full-Text [PDF 1316 kb]
| Abstract (HTML)
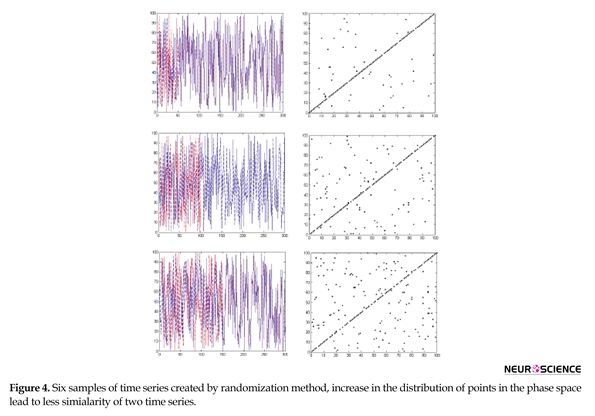
In order to better assess the similarity measures applied in the detection of brain functional connectivity using the graph theory, other surrogate data were generated using the randomization process. In these data, at first two time series were randomly generated. Then, the similarity of these two time series to each other was gradually reduced to a specific amount. In the last phase, similarity measure value on each of these signal pairs by three proposed methods, including linear correlation, mutual information and fractal dimension was calculated. Because in the surrogate data, the similarity of each signal pair has a downward trend, similarity measures, also, have to follow this trend.
2.6. Thresholding method
Presently, for studies on complex brain network, there is no consensus over selection of a specified threshold (Achard & Bullmore, 2007). Pursuant to studies already carried out, each element’s absolute value (positive and negative values were only contained in Pearson’s matrix) was applied as the inter-regional functional connectivity (Bassett et al., 2008; Braun et al., 2012; Wang et al., 2011; Zhang et al., 2011). Ultimately, we thresholded these matrices of adjacency into a binary matrix.
In this study, for the networks properties to be investigated, we employed a range of threshold values, from 0.1 to 0.5, with an increment of 0.1. In this method to derive adjacency matrices, we thresholded them in a proportional manner (i.e. normalization by “wiring cost” – e.g. 0.1 represents 10% of the strongest connections being maintained as links). For each individual, a connectivity matrix of 90×90 was obtained and the topological organization of functional networks of the whole brain analyzed in compliance with graph theory, taking each ROI into account as a node and the functional connectivity as an edge.
2.7. Topological properties of brain networks
Of all the multiple matrices of network we needed to measure for the assessment of the small-world properties (Sporns & Zwi, 2004), the Clustering Coefficient (CC) and the mean minimum Path Length (PL) are regarded to be the major components of the small-world network. The clustering coefficient ratio, 0˂CCi˂1, describes the range or amount of potential connections that the closest neighbors of a node actually has (Liu et al., 2009):
(7)
The total number of nodes of a network, the number of edges by which node j’s neighbors are connected to one another and the number of node j’s neighbors are illustrated by N, #Ej and #Vj in this equation, correspondingly. Moreover, we will have L (i.e. the minimum path length), dividing the shortest path lengths in average by each potential vertices pair:
(8)
In the above formula, the path length is determined by the number of edges the path encompasses. Also delineates the shortest length (i.e. the ith or the jth). The average minimum number of connections linking any two nodes of the network is referred to as the Characteristic Path Length (CPL). Furthermore, we computed, for a CC and CPL graph containing as many nodes as edges, the corresponding parameters, according to what and determine. These random networks were established to obliterate any structure of local adjacency, when the primary level of distribution is kept. This was carried out by each edge being reattached in the original network, 1000 times in average, randomly (Hayasaka & Laurienti, 2010; Newman, Strogatz, & Watts, 2001). Random networks require a shortest path length in average which is small, having limited local interconnections resulting in a small Crand and Lrand. The graph, on the ground that it has a small shortest length in average and its average clustering coefficient is strikingly greater than a constructed random graph on the same number of nodes, would be regarded as small-world. It has been demonstrated that, supporting effective parallel transmission of information at a comparatively low cost, economical small-world properties with high global efficiency (Eglobal) are owned by the brain functional networks. The harmonic mean inverse of the least absolute path length between each nodes pair, is delineated as (Liu et al., 2008).
(9)
For two groups of addicts and normal individuals, clustering coefficient, characteristic path length and efficiency were computed for edge definition using the three methods of LC, MI and BCFD, respectively. It should be noted that the nature of the graphs obtained by these three methods is different to some extent, where LC method quantifies the linear interactions between the nodes, MI calculates the shared information and BCFD computes the self-similarity. Thus, the values of clustering coefficient, path length and efficiency in the graphs obtained by LC and MI and BCFD methods will be different. But, regardless of the nature of these three graphs and the varied values of the features, the interpretation of clustering coefficient, path length and efficiency will be the same in all three graphs.
2.8. Statistical analysis
To evaluate the brain network properties, statistical difference between addict participants and normal controls, a test of non-parametric permutation was applied (He, Chen, & Evans, 2008). In the first place, we calculated the network topological properties inclusive of Clustering Coefficients, Characteristic Path Length (CPL) and Global Efficiency (GE). Next, each individual’s regional cortical thickness measures were assigned to either group randomly. In addition, we recomputed LC, MI and BCFD matrices for each of the 2 groups randomized and, for the network property measure, obtained a new value. We repeated this process of randomization 1000 times. Because less than 5 percentile of intergroup difference in the distribution of permutation is more than the discrepancy in the observed group, the significance would be reached. For each threshold, the procedure was repeated.
3. Result
Investigated from a functional integration viewpoint and in line with LC, MI and BCFD methods, methamphetamine addiction problems were considered through graph topological properties. In order for the network to be built, for both methamphetamine users and normal controls, graph theory was applied, enabling us to analyze the topological properties of functional brain networks between these two groups.
By generating the surrogate data, we aim at evaluating the performance of each method in several pairs of time series, before they are applied for the real data. That is because these methods are used as the similarity measure of two time series from two fMRI voxels. These similarity measures are compared and assessed using the time series with linear and non-linear behavior, about which we have prior knowledge. To evaluate LC, MI and BCFD methods, two surrogate data sets generated by the randomization process (as linear behavior) and by the logistic equation (as a non-linear behavior) were used.
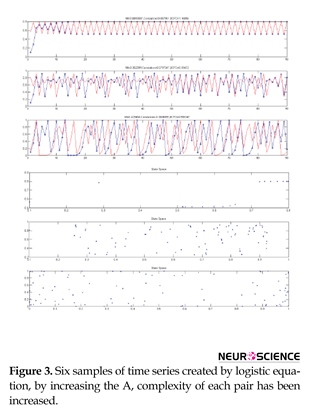
Figure 3 shows the results of creating six time series using logistic equation. Upper signals correspond to less nonlinearity and more linearity and lower signals correspond to more nonlinearity and less linearity. As can be seen, there are a few similarities in the signals. We aim at quantifying these similarities using BCFD and evaluating the results of BCFD versus LC and MI.
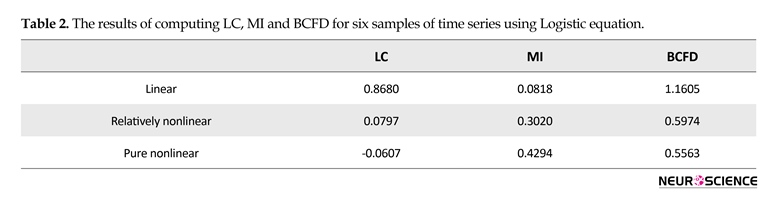
As seen in Figure 3, with an increase in the value of A in logistic equation, complexity increases, interpreted based on an increase in the distribution of points in the phase space, while the similarity and connectivity of the two time series decrease in a non-linear manner. For these six typical time series (3 pairs), linear correlation, mutual information and box counting were executed and the similarity measures were computed. Table 2 displays the results.
As seen in Table 2 and based on the visual comparison, by increasing nonlinearity, LC has no significant changes in the values of these three methods for nonlinear range and just has a good performance in linear range, MI has an increasing trend representing that mutual information functions well just in nonlinear range. Among these three algorithms only BCFD has significant changes and shows the capability of its discrimination for similarity measure in both linear and nonlinear ranges. Figure 4 shows the results of creating six time series using randomization method and corresponding phase spaces. Upper signals correspond to more similarity. By reducing the time series similarity, dispersion of points in phase space has been increased.
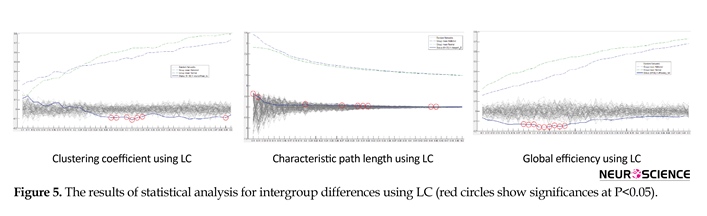
Based on our statistical analysis using BCFD and consistent with several previously conducted studies on addiction, there was a significant difference between groups in global efficiency, clustering coefficient, as well as Characteristic Path Length (CPL) at different thresholds (Ersche et al., 2006; Jiang et al., 2013). Figure 5 depicts CC, CPL and GE schemes of the whole-brain functional network changing with the thresholds in both addict participants and normal controls and obtained with the application of LC, MI and BCFD methods. As can be seen in Figure 5a, Figure 5b and Figure 5c, for LC method, significant differences between groups in CC, CPL and GE were observed. As desired and compared to the random networks, relatively higher CC and GE, except CPL, were exhibited by the networks of addict and normal participants. Thus at the red circle thresholds, there were differences in CC, CPL and GE considered significant (red circles, P<0.05). Only CC and GE of normal subjects valued higher.
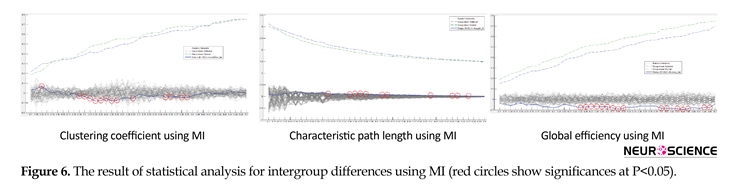
Graph topological properties of both addict subjects and normal controls using MI method is presented in Figure 6a, Figure 6b and Figure 6c. In this respect, similar to the analysis using LC, significant differences at a number of network thresholds for CC, CPL and GE (red circles, P<0.05) were revealed. Conforming to the results, as compared to those of addict subjects, relatively higher CC and GE were exhibited by the networks of normal controls. Furthermore, implying that MI is more robust than LC to extract to the differences in graph topological features, the number of significant differences using MI is more than those through LC method.
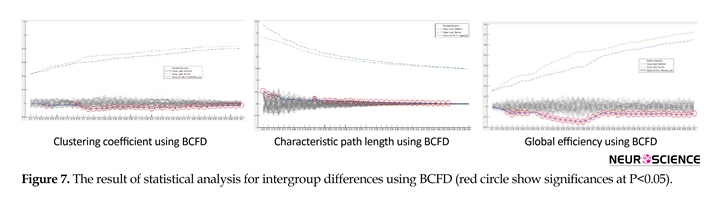
Figure 7 illustrates the statistical analysis of the graph topological properties using BCFD. Once more, identical to the analysis utilizing LC and MI, as compared with normal controls, brain networks of addicted participants display significant differences in CC, CPL and GE. In this method, the number of significant points is observed at a wide range. Thus, BFCD holds more homogenous significant variations insinuating that, compared with normal controls, the differences in addicts’ brain networks in almost all network thresholds can be differentiated by BCFD method and, besides, represent greater validity and reliability of the brain network analysis using graph theory. According to the results, in all circumstances, all three topological features in healthy individuals are more than in addicts, with the exception of CPL, by whom the main hypothesis of this study is asserted to be vindicated.
4. Discussion
A prominent approach to the analysis of fMRI data, in particular the resting state data is Functional Connectivity (FC). Two common methods of functional connectivity analysis are graph theory and seed-based analysis which employ Linear Correlation (LC) measures. An implicit assumption of Gaussianity is applied to the dependence structure by utilizing linear correlation measures (Chang & Glover, 2010). It is of a great importance to bear in mind that non-Gaussianity may result in the false detection of nonstationarity. It should also be kept in mind that, rather than with neuronal activations, we are dealing with the level of fMRI BOLD signal; the non-neural sources of variation are likely to influence, to some extent, the contributions of both the Gaussian and non-Gaussian. Due to generality, a specific position is held by Mutual Information (MI) among a great number of possible nonlinear FC measure candidates. Theoretically, adopting an arbitrary form of dependence association among the variables, without any apriority model limitations on its form, would be general enough. MI features provide us with the opportunity not only to examine the appropriateness of linear correlation for fMRI time series, but also to quantify the information disregarded using linear correlation. Owing to greater sensitivity of MI to higher order statistics considering only the second order (Smith et al., 2011), as compared to LC, an extra amount of information is resulted and the possible contribution of non-linear alternatives over the Pearson correlation coefficient is bounded.
Currently by employing the elements of chaos theory, modern neuroscientists have been able to recognize the fractal properties present in the brain functions (Expert et al., 2011; Papo et al., 2014; You & Stadler, 2012). However, until just the recent time, there was no analytical method for the objective explanation of the brain complexity. However, the question of which interdependence or connectivity measures to be applied is not generally responded. The crucial trade-off factors would probably depend upon a specific dataset and the regarding scientific problem (Hartman et al., 2011).
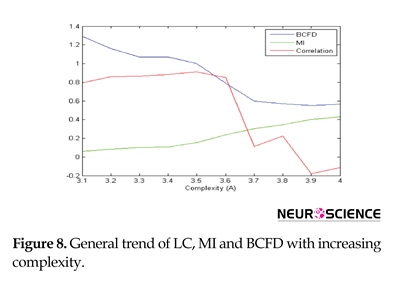
The surrogate data analysis conducted applying the logistic equation may give us the insight to fractal behavior impact on the brain complex networks. Figure 8 displays the performance of these 3 algorithms with increasing the complexity. As desired, correlation has a good performance in only linear range because of its fluctuation. MI has a good performance in only nonlinear, but BCFD performs well in both linear and nonlinear ranges, expressing that BFCD is a better dependency measure for comparing time series to define the edge of graph for graph-centered network analysis of the brain.
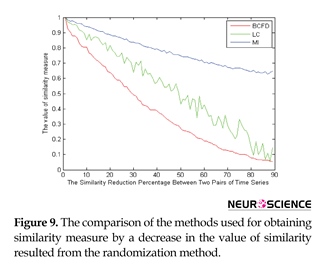
In order to better evaluate the similarity measures applied in the brain functional connectivity using the graph theory, other surrogate data were created using the randomization process. In these data, as shown in Figure 9, in the first step where the two signals are completely similar to one another, their values have to be the maximum value. Since in establishing the random signal pairs, the trend is a monotonic downward trend, the values of similarity measures have to lack fluctuations. The last important point is that, in the last stage, the similarity of the pair of signals would be a specific number; hence, in the last phase, similarity measures should have a value similar to that specific value.
As seen in Figure 9, all the three similarity measures are started from the maximum value, which seems reasonable, knowing that two signal pairs are completely similar. However, compared to the other methods, the Linear Correlation (LC) has more fluctuations, which is not desirable due to less similarity of each signal pair in proportion to the prior signal pair in the surrogate data. In spite of its lower fluctuations, Mutual Information (MI) method does not perform greatly for low similarity values. That is because, in the last stages where the specific value of 30% in the surrogate data, for example, has been already given to the similarity, a much higher value is shown by the use of this measure. Among the similarity measures, Box-Counting Fractal Dimension (BCFD) seems to have been able to follow all the existent behavior, and thus, it can have a better performance for the graph edge determination in brain functional connectivity analyses.
By reducing the similarity value, LC method has a great number of fluctuations and MI follows the variations in the similarity reduction with a very little slope, whereas FD follows the variations in the similarity reduction well. Being repeated 1000 times, the results from the statistical analysis showed no significant difference between LC, MI and FD methods in the data generated through randomization. Similar to the randomization method, we reduce the similarity of the time series to one another in a linear manner, such a conclusion seems reasonable. That is because, in fact, the data still have a linear relationship with each other. However, in the data created by the logistic equation, a significant difference was observed between the three methods. Similarly, this result is not far-fetched, as with an increase in the value of A in the logistic equation, complexity (distribution of points in the phase space), i.e. the non-linear interaction between the time series will increase. Regarding the evidence cited in the surrogate data, it can be concluded that FD seems to be a more appropriate criterion for the graph edge determination in functional connectivity studies. In addition, it is proven that the brain, as a complex structure, is fractal (Papo et al., 2014). To express the brain complexity and present an index for it, the complexity of the time series of fMRI voxels can be investigated between the test group and the control group. An expression of complexity introduced in this study was the point’s distribution of the time series in the phase space, a kind of deviation from the linearity and non-linearity of the interactions between the brain regions of addicts, compared with normal controls, quantified and evaluated using BCFD method. The use of BCFD method for quantifying the complexity of the interactions of fMRI time series and thus, providing a criterion for the brain complexity is a benefit not achievable through the conventional methods of LC and MI. However, applying other concepts to interpret and assess the complexity of the brain requires further studies.
There is a number of well-established circuits characterizing the cognitive impairments of addicted brain; namely decision-making, impulsivity, attention disturbances and assigning emotional valence circuits (Lee & Pau, 2002; Lee et al., 2005; Li & Sinha, 2008; Volkow, Fowler, & Wang, 2003). Studies have also suggested some irregularities in these circuits for methamphetamine dependents (Monterosso, Aron, Cordova, Xu, & London, 2005). To this end, studying these circuits in MDI through a graph theoretical perspective is beneficial. In the current study, alterations were found in MDIs universal parameters of the brain functional networks, in comparison with those of NCs. Statistical analysis revealed a significant decrease in clustering coefficient, global efficiency and small-world indices and increase in characteristic path length of MDIs.
One of the indices characterizing the manner in which the brain networks are shifted to either a regular or a random network is the clustering coefficient (He & Evans, 2010). Studies have previously shown a decreased clustering coefficient in ADHD individuals justifying their attention disorders (Wang, Li, Metzak, He, & Woodward, 2010), this may also be the case for our MDIs as attention deficit is a commonly reported cognitive impairment in meth addiction (Sim et al., 2001).
Universal processing and transfer of information from each brain region to all the other ones is taken into consideration by global efficiency, which, to ensure effective interactions or rapid information transfer over the distant cortical regions involved in the basis of a great number of cognitive processes, predominantly relates the long-range connections (Latora & Marchiori, 2001). Low global efficiency is linked to lower IQ score (Li et al., 2009; Van den Heuvel, Stam, Kahn, & Pol, 2009), which may be due to a slower information process, a critical subscale in IQ score; consistently lower global efficiency can be indicative of decreased information process speed in MDIs.
The mean minimum number of links connecting any two nodes within the network is considered as the characteristic path length of a network. Giving an overview of information transfer effectiveness and measuring the functional integration of the whole brain, the capability for the brain network parallel information propagation is quantified by the characteristic path length of a network (Tschernegg et al., 2013). Obviously, a longer characteristic path length will make for a more time consuming and/or less efficient integration of modules. Increase in characteristic path length in our participants can be a reason for the observed psychomotor retardation of brain functions in abstinent psycho stimulant-dependent individuals (Pulvirenti & Koob, 1993).
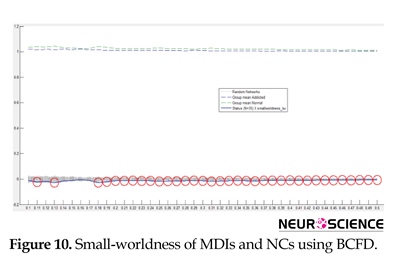
The model of small-world network topology is considered by a high local clustering coefficient and shortest path length (Rubinov & Sporns, 2010). Small-world properties lead to maintaining highly effective, specialized modular information process and fast global information transfer in a network (Kaiser & Hilgetag, 2006). Similar to earlier studies on functional networks of the human brain (Liao et al., 2010; Liu et al., 2008; Supekar et al., 2008; Tian, Wang, Yan, & He, 2011; Zhang et al., 2011), in this study, the small-world properties of MDIs’ and NCs’ resting networks were investigated over a range of threshold values. Statistical comparison of the two groups showed that small-world properties were conserved by both MDIs’ and NCs’ whole-brain functional network. The small-world scalar was smaller in MDIs than the NCs (Figure 10). Small-word property increases through brain development, representing a shift of brain networks towards regularity (Park et al., 2015); indicating improved decision making in adults. Inversely, low small-world scalar in our study may be a reason for common cognitive impairments in MDIs, especially disrupted decision making (Kohno, Morales, Ghahremani, Hellemann, & London, 2014) and impulsive behaviors, a hint of a shift towards randomness.
By comparing the edge definition methods and the features derived from functional connectivity graph, it is concluded that there is a significant difference in the brain network topological features of the addicts, compared to those of the control group; in all three edge definition methods, the difference was obtained in terms of network topological features. The number of significant points, however, are more in BCFD method than in LC and even MI. As stated in Liu et al. study (Liu et al., 2009), the greater number of significant points, regardless of the connectivity threshold, can be a criterion for the comparison of these methods. These materials can certify the proof of the main and sub-hypotheses of this research. 5. Conclusion
According to the gathered body of evidence, a more powerful manner to appreciate the brain networks topological principles is put up by the graph theoretical analysis of neuroimaging data applying BCFD than through LC and MI methods. Using resting-state fMRI and a graph theory method, we aimed at investigating the functional network of the whole-brain in MDIs. As lower clustering coefficient, global efficiency and lessened small-worldness indicate, the whole-brain functional networks in MDIs, compared to those in normal controls, were pointed out to be probably shifted toward random organization.
On the whole, the present study found disruptions in the whole-brain functional networks topological graph properties of MDIs. The findings are valuable to better understand the underlying mechanisms of addiction. Due to such efforts, recently developed research areas of interest to all basic scientists and clinical researchers are being opened up into organizational mechanisms of the brain. Considering the features of graph theory in establishment of network alterations, it seems to be a suitable biomarker for monitoring addiction treatment and detecting the treatment progress ahead of significant clinical symptoms.
Acknowledgements
This study has been financially supported by Tehran University of Medical Sciences (Grant No: 20125).
Conflict of Interest
All authors certify that this manuscript has neither been published in whole nor in part nor being considered for publication elsewhere. The authors have no conflicts of interest to declare.
References
Achard, S., & Bullmore, E. (2007). Efficiency and cost of economical brain functional networks. PLoS Computational Biology, 3(2), 17. doi: 10.1371/journal.pcbi.0030017
Ahmadi, K., Ahmadlou, M., Rezazade, M., Azad-Marzabadi, E., & Sajedi, F. (2013). Brain activity of women is more fractal than men. Neuroscience Letters, 535, 7-11. doi: /10.1016/j.neulet.2012.12.043
Ahmadlou, M., & Adeli, H. (2011). Functional community analysis of brain: a new approach for EEG-based investigation of the brain pathology. Neuroimage, 58(2), 401-408. doi: 10.1016/j.neuroimage.2011.04.070
Ahmadlou, M., Ahmadi, K., Rezazade, M., & Azad-Marzabadi, E. (2013). Global organization of functional brain connectivity in methamphetamine abusers. Clinical Neurophysiology, 124(6), 1122-31. doi: 10.1016/j.clinph.2012.12.003
Arora, S., & Santhanam, M. (2014). Synchronization of coupled map lattice using delayed variable feedback. Journal of Applied Nonlinear Dynamics, 3(3), 245-53. doi: 10.5890/jand.2014.09.004
Bassett, D. S., Bullmore, E., Verchinski, B. A., Mattay, V. S., Weinberger, D. R., & Meyer-Lindenberg, A. (2008). Hierarchical organization of human cortical networks in health and schizophrenia. Journal of Neuroscience, 28(37), 9239-48. doi: 10.1523/jneurosci.1929-08.2008
Bassett, D. S., & Bullmore, E. T. (2009). Human brain networks in health and disease. Current Opinion in Neurology, 22(4), 340-47. doi: 10.1097/wco.0b013e32832d93dd
Bergfeldt, U., Jonsson, T., Bergfeldt, L., & Julin, P. (2015). Cortical activation changes and improved motor function in stroke patients after focal spasticity therapy–an interventional study applying repeated fMRI. BMC Neurology, 15(1), 52. doi: 10.1186/s12883-015-0306-4
Bollobás, B. (1998). Modern graph theory (Vol. 184). Berlin: Springer Science & Business Media.
Bonita, J., Ambolode II, L., Rosenberg, B., Cellucci, C., Watanabe, T., Rapp, P., et al. (2014). Time domain measures of inter-channel EEG correlations: A comparison of linear, nonparametric and nonlinear measures. Cognitive Neurodynamics, 8(1), 1-15. doi: 10.1007/s11571-013-9267-8
Braun, U., Plichta, M. M., Esslinger, C., Sauer, C., Haddad, L., Grimm, O., et al. (2012). Test–retest reliability of resting-state connectivity network characteristics using fMRI and graph theoretical measures. Neuroimage, 59(2), 1404-12. doi: 10.1016/j.neuroimage.2011.08.044
Bullmore, E., & Sporns, O. (2009). Complex brain networks: graph theoretical analysis of structural and functional systems. Nature Reviews Neuroscience, 10(3), 186-198. doi: 10.1038/nrn2575
Cabral, J., Kringelbach, M., & Deco, G. (2012). Functional graph alterations in schizophrenia: A result from a global anatomic decoupling? Pharmacopsychiatry, 45(S01), S57-S64. doi: 10.1055/s-0032-1309001
Chang, C., & Glover, G. H. (2010). Time–frequency dynamics of resting-state brain connectivity measured with fMRI. Neuroimage, 50(1), 81-98. doi: 10.1016/j.neuroimage.2009.12.011
Chao-Gan, Y., & Yu-Feng, Z. (2010). DPARSF: A MATLAB toolbox for “pipeline” data analysis of resting-state fMRI. Frontiers in System Neuroscience, 4. doi: 10.3389/fnsys.2010.00013
Culham, J. C., & Kanwisher, N. G. (2001). Neuroimaging of cognitive functions in human parietal cortex. Current Opinion in Neurobiology, 11(2), 157-163. doi: 10.1016/s0959-4388(00)00191-4
Deuker, L., Bullmore, E. T., Smith, M., Christensen, S., Nathan, P. J., Rockstroh, B., et al. (2009). Reproducibility of graph metrics of human brain functional networks. Neuroimage, 47(4), 1460-68. doi: 10.1016/j.neuroimage.2009.05.035
Donges, J. F., Zou, Y., Marwan, N., & Kurths, J. (2009). Complex networks in climate dynamics. The European Physical Journal Special Topics, 174(1), 157-179. doi: 10.1140/epjst/e2009-01098-2
Ersche, K. D., Fletcher, P. C., Roiser, J. P., Fryer, T. D., London, M., Robbins, T. W., et al. (2006). Differences in orbitofrontal activation during decision-making between methadone-maintained opiate users, heroin users and healthy volunteers. Psychopharmacology, 188(3), 364-373. doi: 10.1007/s00213-006-0515-z
Expert, P., Lambiotte, R., Chialvo, D. R., Christensen, K., Jensen, H. J., Sharp, D. J., et al. (2011). Self-similar correlation function in brain resting-state functional magnetic resonance imaging. Journal of The Royal Society Interface, 8(57), 472-479. doi: 10.1098/rsif.2010.0416
Fransson, P. (2005). Spontaneous low‐frequency BOLD signal fluctuations: An fMRI investigation of the resting‐state default mode of brain function hypothesis. Human Brain Mapping, 26(1), 15-29. doi: 10.1002/hbm.20113
Gómez, C. M., Vaquero, E., López-Mendoza, D., González-Rosa, J., & Vázquez-Marrufo, M. (2004). Reduction of EEG power during expectancy periods in humans. Acta Neurobiologiae Experimentalis, 64(2), 143-51. PMID: 15366247
Hartman, D., Hlinka, J., Paluš, M., Mantini, D., & Corbetta, M. (2011). The role of nonlinearity in computing graph-theoretical properties of resting-state functional magnetic resonance imaging brain networks. Chaos: An Interdisciplinary Journal of Nonlinear Science, 21(1), 013119. doi: 10.1063/1.3553181
Hayasaka, S., & Laurienti, P. J. (2010). Comparison of characteristics between region-and voxel-based network analyses in resting-state fMRI data. Neuroimage, 50(2), 499-508. doi: 10.1016/j.neuroimage.2009.12.051
He, Y., Chen, Z., & Evans, A. (2008). Structural insights into aberrant topological patterns of large-scale cortical networks in Alzheimer’s disease. Journal of Neuroscience, 28(18), 4756-66. doi: 10.1523/jneurosci.0141-08.2008
He, Y., & Evans, A. (2010). Graph theoretical modeling of brain connectivity. Current Opinion in Neurology, 23(4), 341-350. doi: 10.1097/wco.0b013e32833aa567
Hlinka, J., Paluš, M., Vejmelka, M., Mantini, D., & Corbetta, M. (2011). Functional connectivity in resting-state fMRI: is linear correlation sufficient? Neuroimage, 54(3), 2218-25. doi: 10.1016/j.neuroimage.2010.08.042
Jiang, G., Wen, X., Qiu, Y., Zhang, R., Wang, J., Li, M., et al. (2013). Disrupted topological organization in whole-brain functional networks of heroin-dependent individuals: A resting-state FMRI study. PLoS ONE, 8(12), e82715. doi: 10.1371/journal.pone.0082715
Kaiser, M., & Hilgetag, C. C. (2006). Nonoptimal component placement, but short processing paths, due to long-distance projections in neural systems. PLoS Computational Biology, 2(7), e95. doi: 10.1371/journal.pcbi.0020095
Khan, S., Bandyopadhyay, S., Ganguly, A. R., Saigal, S., Erickson III, D. J., Protopopescu, V., et al. (2007). Relative performance of mutual information estimation methods for quantifying the dependence among short and noisy data. Physical Review E, 76(2), 026209. doi: 10.1103/physreve.76.026209
Kohno, M., Morales, A. M., Ghahremani, D. G., Hellemann, G., & London, E. D. (2014). Risky decision making, prefrontal cortex, and mesocorticolimbic functional connectivity in methamphetamine dependence. JAMA psychiatry, 71(7), 812-820. doi: 10.1001/jamapsychiatry.2014.399
Kreuz, T., Mormann, F., Andrzejak, R. G., Kraskov, A., Lehnertz, K., & Grassberger, P. (2007). Measuring synchronization in coupled model systems: A comparison of different approaches. Physica D: Nonlinear Phenomena, 225(1), 29-42. doi: 10.1016/j.physd.2006.09.039
Latora, V., & Marchiori, M. (2001). Efficient behavior of small-world networks. Physical Review Letters, 87(19), 198701. doi: 10.1103/physrevlett.87.198701
Lee, T. M., & Pau, C. W. (2002). Impulse control differences between abstinent heroin users and matched controls. Brain Injury, 16(10), 885-89. doi: 10.1080/02699050210128915
Lee, T. M., Zhou, W. H., Luo, X. J., Yuen, K. S., Ruan, X. Z., & Weng, X. C. (2005). Neural activity associated with cognitive regulation in heroin users: A fMRI study. Neuroscience Letters, 382(3), 211-216. doi: 10.1016/j.neulet.2005.03.053
Li, C. S. R., & Sinha, R. (2008). Inhibitory control and emotional stress regulation: neuroimaging evidence for frontal–limbic dysfunction in psycho-stimulant addiction. Neuroscience & Biobehavioral Reviews, 32(3), 581-597. doi: 10.1016/j.neubiorev.2007.10.003
Li, J., Du, Q., & Sun, C. (2009). An improved box-counting method for image fractal dimension estimation. Pattern Recognition, 42(11), 2460-69. doi: 10.1016/j.patcog.2009.03.001
Li, Y., Liu, Y., Li, J., Qin, W., Li, K., Yu, C., et al. (2009). Brain anatomical network and intelligence. PLoS Computational Biology, 5(5), e1000395. doi: 10.1371/journal.pcbi.1000395
Liao, W., Zhang, Z., Pan, Z., Mantini, D., Ding, J., Duan, X., et al. (2010). Altered functional connectivity and small-world in mesial temporal lobe epilepsy. PLoS ONE, 5(1), e8525. doi: 10.1371/journal.pone.0008525
Liu, J., Liang, J., Qin, W., Tian, J., Yuan, K., Bai, L., et al. (2009). Dysfunctional connectivity patterns in chronic heroin users: An fMRI study. Neuroscience Letters, 460(1), 72-77. doi: 10.1016/j.neulet.2009.05.038
Liu, Y., Liang, M., Zhou, Y., He, Y., Hao, Y., Song, M., et al. (2008). Disrupted small-world networks in schizophrenia. Brain, 131(4), 945-961. doi: 10.1093/brain/awn018
Mamashli, F., Ahmadlu, M., Golpayegani, M. R., Gharibzadeh, S. (2010). Detection of attention using chaotic global features. Journal of Neuropsychiatry and Clinical Neurosciences, 22(2), E20. doi: 10.1176/jnp.2010.22.2.247.e20
Monterosso, J. R., Aron, A. R., Cordova, X., Xu, J., & London, E. D. (2005). Deficits in response inhibition associated with chronic methamphetamine abuse. Drug and Alcohol Dependence, 79(2), 273-77. doi: 10.1016/j.drugalcdep.2005.02.002
Nakamura, T., Hillary, F. G., & Biswal, B. B. (2009). Resting network plasticity following brain injury. PLoS ONE, 4(12), e8220. doi: 10.1371/journal.pone.0008220
Newman, M. E., Strogatz, S. H., & Watts, D. J. (2001). Random graphs with arbitrary degree distributions and their applications. Physical Review E, 64(2), 026118. doi: 10.1103/physreve.64.026118
Papo, D., Zanin, M., & Buldú, J. M. (2014). Reconstructing functional brain networks: Have we got the basics right? Frontiers in Human Neuroscience, 8. doi: 10.3389/fnhum.2014.00107
Park, C. h., Chun, J. W., Cho, H., Jung, Y. C., Choi, J., & Kim, D. J. (2015). Is the Internet gaming‐addicted brain close to be in a pathological state? Addiction Biology, 22(1), 196-205. doi: 10.1111/adb.12282
Ponten, S., Bartolomei, F., & Stam, C. (2007). Small-world networks and epilepsy: Graph theoretical analysis of intracerebrally recorded mesial temporal lobe seizures. Clinical Neurophysiology, 118(4), 918-27. doi: 10.1016/j.clinph.2006.12.002
Pulvirenti, L., & Koob, G. F. (1993). Lisuride reduces psychomotor retardation during withdrawal from chronic intravenous amphetamine self-administration in rats. Neuropsychopharmacology, 8(3), 213-18. doi: 10.1038/npp.1993.23
Rubinov, M., & Sporns, O. (2010). Complex network measures of brain connectivity: Uses and interpretations. Neuroimage, 52(3), 1059-69. doi: 10.1016/j.neuroimage.2009.10.003
Sim, T., Simon, S. L., Domier, C. P., Richardson, K., Rawson, R. A., & Ling, W. (2001). Cognitive deficits among methamphetamine users with attention deficit hyperactivity disorder symptomatology. Journal of Addictive Diseases, 21(1), 75-89. doi: 10.1300/j069v21n01_07
Smith, S. M., Matthews, P. M., & Jezzard, P. (2001). Functional MRI: An introduction to methods. Oxford: Oxford University Press.
Smith, S. M., Miller, K. L., Salimi-Khorshidi, G., Webster, M., Beckmann, C. F., Nichols, T. E., et al. (2011). Network modelling methods for FMRI. Neuroimage, 54(2), 875-891. doi: 10.1016/j.neuroimage.2010.08.063
Sporns, O. (2006). Small-world connectivity, motif composition, and complexity of fractal neuronal connections. Biosystems, 85(1), 55-64. doi: 10.1016/j.biosystems.2006.02.008
Sporns, O., & Zwi, J. D. (2004). The small world of the cerebral cortex. Neuroinformatics, 2(2), 145-162. doi: doi.org/10.1385/ni:2:2:145
Sun, J., Tong, S., & Yang, G. Y. (2012). Reorganization of brain networks in aging and age-related diseases. Aging and disease, 3(2), 181-93. PMID: 22724079
Supekar, K., Menon, V., Rubin, D., Musen, M., & Greicius, M. D. (2008). Network analysis of intrinsic functional brain connectivity in Alzheimer’s disease. PLoS Computational Biology, 4(6), e1000100. doi: 10.1371/journal.pcbi.1000100
Sutherland, M. T., McHugh, M. J., Pariyadath, V., & Stein, E. A. (2012). Resting state functional connectivity in addiction: Lessons learned and a road ahead. Neuroimage, 62(4), 2281-95. doi: 10.1016/j.neuroimage.2012.01.117
Tian, L., Wang, J., Yan, C., & He, Y. (2011). Hemisphere-and gender-related differences in small-world brain networks: A resting-state functional MRI study. Neuroimage, 54(1), 191-202. doi: 10.1016/j.neuroimage.2010.07.066
Tschernegg, M., Crone, J. S., Eigenberger, T., Schwartenbeck, P., Fauth-Bühler, M., Lemènager, T., et al. (2013). Abnormalities of functional brain networks in pathological gambling: A graph-theoretical approach. Frontiers in Human Neuroscience, 7. doi: 10.3389/fnhum.2013.00625
Tzourio-Mazoyer, N., Landeau, B., Papathanassiou, D., Crivello, F., Etard, O., Delcroix, N., et al. (2002). Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage, 15(1), 273-89. doi: 10.1006/nimg.2001.0978
Van den Heuvel, M. P., Stam, C. J., Kahn, R. S., & Pol, H. E. H. (2009). Efficiency of functional brain networks and intellectual performance. Journal of Neuroscience, 29(23), 7619-24. doi: 10.1523/jneurosci.1443-09.2009
Volkow, N. D., Fowler, J. S., & Wang, G. J. (2003). The addicted human brain: Insights from imaging studies. Journal of Clinical Investigation, 111(10), 1444-51. doi: 10.1172/jci200318533
Wang, J. H., Zuo, X. N., Gohel, S., Milham, M. P., Biswal, B. B., & He, Y. (2011). Graph theoretical analysis of functional brain networks: test-retest evaluation on short-and long-term resting-state functional MRI data. PLoS ONE, 6(7), e21976. doi: 10.1371/journal.pone.0021976
Wang, J., Wang, L., Zang, Y., Yang, H., Tang, H., Gong, Q., et al. (2009). Parcellation‐dependent small‐world brain functional networks: A resting‐state fMRI study. Human Brain Mapping, 30(5), 1511-23. doi: 10.1002/hbm.20623
Wang, L., Li, Y., Metzak, P., He, Y., & Woodward, T. S. (2010). Age-related changes in topological patterns of large-scale brain functional networks during memory encoding and recognition. Neuroimage, 50(3), 862-72. doi: 10.1016/j.neuroimage.2010.01.044
Ward, B. D., & Mazaheri, Y. (2008). Information transfer rate in fMRI experiments measured using mutual information theory. Journal of Neuroscience Methods, 167(1), 22-30. doi: 10.1016/j.jneumeth.2007.06.027
Warsi, M. A. (2012). The Fractal Nature and Functional Connectivity of Brain Function as Measured by BOLD MRI in Alzheimer’s Disease [PhD thesis]. Hamilton: McMaster University.
Xia, M., & He, Y. (2011). Magnetic resonance imaging and graph theoretical analysis of complex brain networks in neuropsychiatric disorders. Brain Connectivity, 1(5), 349-65. doi: 10.1089/brain.2011.0062
You, W., & Stadler, J. (2012). Fractal-driven distortion of resting state functional networks in fMRI: A simulation study. Paper presented at The 3rd Biennial Conference on Resting State Brain Connectivity, Magdeburg, Germany, 5-7 September 2012.
Zhang, J., Wang, J., Wu, Q., Kuang, W., Huang, X., He, Y., et al. (2011). Disrupted brain connectivity networks in drug-naive, first-episode major depressive disorder. Biological Psychiatry, 70(4), 334-342. doi: 10.1016/j.biopsych.2011.05.018
Zhang, Y., Liu, J., Li, L., Du, M., Fang, W., Wang, D., et al. (2014). A study on small-world brain functional networks altered by postherpetic neuralgia. Magnetic Resonance Imaging, 32(4), 359-365. doi: 10.1016/j.mri.2013.12.016
Zhang, Z., Liao, W., Chen, H., Mantini, D., Ding, J. R., Xu, Q., et al. (2011). Altered functional–structural coupling of large-scale brain networks in idiopathic generalized epilepsy. Brain, 134(10), 2912-28. doi: 10.1093/brain/awr223
Full-Text:
1. Introduction
Among the most intricate networks in nature is the human brain, which transports signals between specific brain regions and responds to external stimuli. The study of brain connectivity, therefore, depends to a great extent, on the comprehension of brain functions and pathology (Sporns & Zwi, 2004).
Functional Magnetic Resonance Imaging (fMRI) is an imaging technique applied to study human brain function and neurological diseases (Smith, Matthews, & Jezzard, 2001). Blood Oxygenation Level Dependent (BOLD) contrast, on the basis of varied magnetic properties of oxygenated (diamagnetic) and deoxygenated (paramagnetic) blood, is applied by well-liked techniques in fMRI (Fransson, 2005). fMRI benefits over the other functional imaging modalities, namely Electro Encephalography (EEG), Magneto Encephalography (MEG) and Positron Emission Tomography (PET) comprise its non-invasiveness, better spatial resolution compared to other modalities and short-time image attainment (Culham & Kanwisher, 2001).
In literature, the term “network” has various definitions. In graph theory and complex networks, ‘‘network’’ bluntly implies a set of nodes and pair-wise edges, by which the nodes are connected. This sense is referred to as Graph theoretical analysis of brain networks. ‘‘Network’’, in neuroimaging, may designate a group of voxels or Regions of Interest (ROIs), that at resting state or in specific cognitive tasks, act identically (Sun, Tong, & Yang, 2012).
From the standpoint of complex networks, there has been a growing interest, over the recent years, in studying the wide-ranging brain activity interaction structure with the use of graph theory and centered on fMRI in the areas of addiction (Sutherland, McHugh, Pariyadath, & Stein, 2012), schizophrenia (Cabral, Kringelbach, & Deco, 2012), brain injury (Nakamura, Hillary, & Biswal, 2009), neuralgia (Zhang et al., 2014), epilepsy (Ponten, Bartolomei, & Stam, 2007), Alzheimer (Supekar, Menon, Rubin, Musen, & Greicius, 2008) and the like (Bullmore & Sporns, 2009).
A brain network, in graph theoretical analyses of fMRI data, is taken into account as an undirected graph, G=(V, E), where a node/vertex (V) in the graph delineates a brain region (i.e. ROI) and an edge/link (E) between two nodes is indicative of brain regions being functionally connected (Deuker et al., 2009).
To create a graph, the concept and also the definition of the edge is a challenging stage. The edge definition methods and the importance of each is well evaluated and tested in Smith study (Smith et al., 2011).
However, to assess the interaction strength between two brain regions for the edge definition, the LC (Pearson) coefficient of corresponding time series is most commonly utilized in functional connectivity studies, substantially in addiction research studies (Xia & He, 2011). The drawback of such a choice may be that the linear correlation does not take into account the nonlinear dependences possibly occurring in the data. While linear measures, including the Pearson correlation coefficient or coherence are frequently applied, increased attention is being paid to potential benefits of nonlinear measures (Donges, Zou, Marwan, & Kurths, 2009; Kreuz et al., 2007). Mutual Information (MI) can establish a nonlinear relationship between fMRI time series and provides an effective pure nonlinear noise-robust correlation measure (Bassett & Bullmore, 2009).
Research studies contemplating nonlinearity as an inherent feature of the brain dynamics are getting continuously more interested in nonlinear approaches toward the analysis of the brain signals, especially those measures in accord with the analysis of chaotic non-linear dynamical systems to analyze the resting state fMRI data, signifying that the presupposition of linearity might be oversimplifying (Hlinka, Paluš, Vejmelka, Mantini, & Corbetta, 2011). On the other hand, the brain, with fractal structure complexity, is best modeled as a complex system (Papo, Zanin, & Buldú, 2014). For the complexity of the brain signal, we can also assess the resting BOLD fMRI time series (Warsi, 2012). The fMRI time series within any given voxel, rather than correlating the brain areas connectivity with the use of measures of linearity and nonlinearity, can reveal the resting state brain functional network complexity. By complexity we mean the spatial distribution of fMRI signals phase that should not be confused with brain complexity.
The most frequently applied method for analyzing the physiological signals complexity is fractal analysis (Ahmadi, Ahmadlou, Rezazade, Azad-Marzabadi, & Sajedi, 2013). Fractal Dimension (FD) analysis is likely to include new information on the functional connectivity of the brain (Sporns, 2006). This information is not attained by applying any traditional linear, as well as nonlinear measures. However, it should be noted that selection of the appropriate method to determine the graph edges in functional connectivity studies and the impact of each
Among the most intricate networks in nature is the human brain, which transports signals between specific brain regions and responds to external stimuli. The study of brain connectivity, therefore, depends to a great extent, on the comprehension of brain functions and pathology (Sporns & Zwi, 2004).
Functional Magnetic Resonance Imaging (fMRI) is an imaging technique applied to study human brain function and neurological diseases (Smith, Matthews, & Jezzard, 2001). Blood Oxygenation Level Dependent (BOLD) contrast, on the basis of varied magnetic properties of oxygenated (diamagnetic) and deoxygenated (paramagnetic) blood, is applied by well-liked techniques in fMRI (Fransson, 2005). fMRI benefits over the other functional imaging modalities, namely Electro Encephalography (EEG), Magneto Encephalography (MEG) and Positron Emission Tomography (PET) comprise its non-invasiveness, better spatial resolution compared to other modalities and short-time image attainment (Culham & Kanwisher, 2001).
In literature, the term “network” has various definitions. In graph theory and complex networks, ‘‘network’’ bluntly implies a set of nodes and pair-wise edges, by which the nodes are connected. This sense is referred to as Graph theoretical analysis of brain networks. ‘‘Network’’, in neuroimaging, may designate a group of voxels or Regions of Interest (ROIs), that at resting state or in specific cognitive tasks, act identically (Sun, Tong, & Yang, 2012).
From the standpoint of complex networks, there has been a growing interest, over the recent years, in studying the wide-ranging brain activity interaction structure with the use of graph theory and centered on fMRI in the areas of addiction (Sutherland, McHugh, Pariyadath, & Stein, 2012), schizophrenia (Cabral, Kringelbach, & Deco, 2012), brain injury (Nakamura, Hillary, & Biswal, 2009), neuralgia (Zhang et al., 2014), epilepsy (Ponten, Bartolomei, & Stam, 2007), Alzheimer (Supekar, Menon, Rubin, Musen, & Greicius, 2008) and the like (Bullmore & Sporns, 2009).
A brain network, in graph theoretical analyses of fMRI data, is taken into account as an undirected graph, G=(V, E), where a node/vertex (V) in the graph delineates a brain region (i.e. ROI) and an edge/link (E) between two nodes is indicative of brain regions being functionally connected (Deuker et al., 2009).
To create a graph, the concept and also the definition of the edge is a challenging stage. The edge definition methods and the importance of each is well evaluated and tested in Smith study (Smith et al., 2011).
However, to assess the interaction strength between two brain regions for the edge definition, the LC (Pearson) coefficient of corresponding time series is most commonly utilized in functional connectivity studies, substantially in addiction research studies (Xia & He, 2011). The drawback of such a choice may be that the linear correlation does not take into account the nonlinear dependences possibly occurring in the data. While linear measures, including the Pearson correlation coefficient or coherence are frequently applied, increased attention is being paid to potential benefits of nonlinear measures (Donges, Zou, Marwan, & Kurths, 2009; Kreuz et al., 2007). Mutual Information (MI) can establish a nonlinear relationship between fMRI time series and provides an effective pure nonlinear noise-robust correlation measure (Bassett & Bullmore, 2009).
Research studies contemplating nonlinearity as an inherent feature of the brain dynamics are getting continuously more interested in nonlinear approaches toward the analysis of the brain signals, especially those measures in accord with the analysis of chaotic non-linear dynamical systems to analyze the resting state fMRI data, signifying that the presupposition of linearity might be oversimplifying (Hlinka, Paluš, Vejmelka, Mantini, & Corbetta, 2011). On the other hand, the brain, with fractal structure complexity, is best modeled as a complex system (Papo, Zanin, & Buldú, 2014). For the complexity of the brain signal, we can also assess the resting BOLD fMRI time series (Warsi, 2012). The fMRI time series within any given voxel, rather than correlating the brain areas connectivity with the use of measures of linearity and nonlinearity, can reveal the resting state brain functional network complexity. By complexity we mean the spatial distribution of fMRI signals phase that should not be confused with brain complexity.
The most frequently applied method for analyzing the physiological signals complexity is fractal analysis (Ahmadi, Ahmadlou, Rezazade, Azad-Marzabadi, & Sajedi, 2013). Fractal Dimension (FD) analysis is likely to include new information on the functional connectivity of the brain (Sporns, 2006). This information is not attained by applying any traditional linear, as well as nonlinear measures. However, it should be noted that selection of the appropriate method to determine the graph edges in functional connectivity studies and the impact of each
edge-determination method on the network topological features is not fully determined yet (Papo et al., 2014).
In this study, the main hypothesis is that the features extracted from the graph theory-based brain network in methamphetamine abusers, compared to healthy individuals, are subjected to modifications. Another hypothesis investigated in this study was that among the edge-definition criteria (LC, MI and BCFD) which will have a better performance, regardless of the connectivity threshold, to differentiate the topological features extracted from the brain networks of the addicts and the control group.
2. Methods
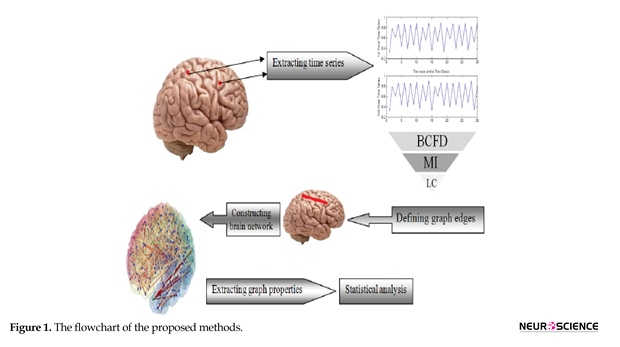
The flowchart of the proposed method, including data acquisition, data preprocessing, functional graph construction, topological graph properties and statistics is depicted in Figure 1. As shown in it, in the first phase, fMRI data are acquired and processed and time series are extracted. Then, using LC, MI and BCFD, the edges
In this study, the main hypothesis is that the features extracted from the graph theory-based brain network in methamphetamine abusers, compared to healthy individuals, are subjected to modifications. Another hypothesis investigated in this study was that among the edge-definition criteria (LC, MI and BCFD) which will have a better performance, regardless of the connectivity threshold, to differentiate the topological features extracted from the brain networks of the addicts and the control group.
2. Methods
The flowchart of the proposed method, including data acquisition, data preprocessing, functional graph construction, topological graph properties and statistics is depicted in Figure 1. As shown in it, in the first phase, fMRI data are acquired and processed and time series are extracted. Then, using LC, MI and BCFD, the edges
are defined and the brain network is constructed. Finally, statistical analysis is performed. Each phase is distinctly stipulated in the following sections.
2.1. Subjects
A total of 18 normal controls (NCs: 18, aged 23–46 years, mean±SD=31.67±7.98 years, right-handed) were enlisted from the local community. Additionally, we enrolled 17 age-matched methamphetamine-dependent individuals (MDIs: 17 Males, aged 22–39 years, mean±SD=30.52±4.57 years, right-handed). Demographic and clinical information regarding MDIs is demonstrated in Table 1. Mann-Whitney U test (Bergfeldt, Jonsson, Bergfeldt, & Julin, 2015) showed no significant difference between MDIs and NCs (P=0.85).
All subjects were capable to realize and follow the protocol of the study during imaging. Neither MDIs nor NCs had any history of pain, neurologic or psychiatric disorders, head injuries, schizophrenia or an affective disorder, in line with their medical history. The present paper was performed in agreement with the Helsinki Declaration also, confirmed by the Research Ethics Review Board of Tehran University of Medical Sciences in Tehran, Iran. Prior to the MRI scanning, informed written consent was obtained from each subject.
2.2. Data acquisition
On a 3 Tesla Siemens Tim Trio scanner, MRI data were acquired in Medical Imaging Department at Imam Khomeini Hospital, Tehran, Iran. To acquire data for Resting-State Magnetic Resonance Imaging (RS-fMRI), a T2*-weighted gradient-echo Echo-Planar Imaging (EPI) sequence was used with the following parameters: Time of Repetition (TR)=3000 ms, Time of Echo (TE)=30 ms, flip angle=90°, matrix=64×64, field of view (FOV)=192 mm2, thickness/gap=4.5 mm, 22 axial slices covering the whole brain and 240 volumes attained in almost 8 minutes. Besides, via a T1-weighted 3D turbo-gradient-echo sequence (TR=1800 ms, TE=30 ms, flip angle=90°, matrix=256×256, FOV=230×230 mm2, thickness=1.0 mm, and 160 sagittal slices), brain structural images with 3D high resolution were obtained. The participants were supposed to have their eyes closed, keep calm, not to systematically think about anything, and not to fall asleep. None of the lights in the scanner room were on during the RS-fMRI scanning.
2.3. Data preprocessing
All the fMRI data were preprocessed using MATLAB software and DPARSF_V2.0 Toolbox (Chao-Gan & Yu-Feng, 2010). For each individual, in the first place, the first 10 volume images were excluded from the RS-fMRI data to make the subjects adapt to the environment and to stabilize the scanner, letting 260 volumes remain for supplementary analysis. Then, to correct the acquisition time delay between slices within the similar TR, slice timing was administered. After that, for the correction of the inter-TR head motions, realignment to the first volume was done. Next, we spatially normalized the fMRI data to a standard Montreal Neurological Institute (MNI) (Tzourio-Mazoyer et al., 2002) template and implemented resampling to a voxel size of 36×63 mm3. According to the studies conducted so far, no spatial smoothing was applied (Achard & Bullmore, 2007; Braun et al., 2012; Wang et al., 2009). Eventually, to reduce the low-frequency drift and high-frequency physiological noise, band-pass filtering was performed for each voxel at the frequency of 0.01–0.08 Hz. The RS-fMRI data for each subject were checked for head motion. In accord with the criteria that the translation and rotation of head motion in any direction were not more than 1.5 mm or 1.5, none of the subjects were disqualified.
2.4. Graph construction
Topological properties of the brain were investigated through the method of binary graph G=(V, E), where a brain region (i.e. ROI) and an edge (E) between two nodes in the graph are indicated by a node/vertex (V). All the regarded graphs in this work are undirected. To analyze complex network, we applied a simple generalization of the graph called weighted graph (Bollobás, 1998).
In this paper, based on the previously conducted studies, two common methods (i.e. LC (Hlinka et al., 2011)and MI (Hartman, Hlinka, Paluš, Mantini, & Corbetta, 2011)), as well as the proposed method (i.e. BCFD) were applied for edge definition. For graph construction, node and edge need to be defined, each of which is explained in detail as follows:
2.4.1. Node definition
In order to have the brain parcellated into 90 Regions Of Interest (ROIs) (45 in each hemisphere), an Automated Anatomical Labeling (AAL) atlas (Tzourio-Mazoyer et al., 2002) was utilized to construct the brain functional networks for each participant.
2.4.2. Edge definition
At this stage, the connectivity, dependence and interactions between the brain regions, i.e. the graph nodes, have to be quantified. Edge definition phase to create graph functional connectivity is challenging to some extent, for which various methods, including linear and nonlinear are presented so far (Ahmadlou & Adeli, 2011; Ahmadlou, Ahmadi, Rezazade, & Azad-Marzabadi, 2013). It should be noted that the method considered as the best method for edge definition and as the edge definition gold standard is still a questionable issue (Papo et al., 2014). According to the previous studies, we used LC and MI methods as the representatives of the linear and non-linear methods, respectively, together with the proposed method “BCFD” for quantifying the interactions between 90 regions selected as nodes based on AAL Atlas. Then, BCFD method was evaluated in comparison with LC and MI. To quantify the nodes connectivity, each of these three methods considers a different criterion.
LC method quantifies the interactions between the time series of each node with linearity supposition, while MI lacks the assumption of the linearity between the brain regions and proposes an index for the evaluation of the shared information between the two time series. But this method is sensitive to the length of time series being analyzed. Since, in functional connectivity studies, the length of time series is usually short, MI use can be somewhat challenging. BCFD was applied in the current study, as it is based on the concept of self-similarity and complexity, i.e. distribution of the points in the phase space, calculating the connectivity and interactions of the brain regions. In addition, it does not assume interactions linearity or sensitive to the length of the time series. The concepts of “self-similarity” and “complexity” have not been evaluated using the graph theory in the functional connectivity studies. We computed the time series for each ROI, by averaging the signals of all voxels within that region. By calculating the Pearson correlation coefficient, MI and BCFD in the residual time courses between all ROI-pairs, a 90×90 adjacency matrix was attained for each subject.
2.4.2.1. Pearson correlation coefficient
A value for the linear association between the time series to be quantified is Pearson correlation, by which the dependence structure Gaussianity presupposition is given. Regarding {X}={x1,x2,xND} and {Y}={y1,y2,yND} as the voxel’s time series, the number of components in each set would be. You will get the Pearson correlation coefficient r as the following equation (Gómez, Vaquero, López-Mendoza, González-Rosa, & Vázquez-Marrufo, 2004) in which is the mean of X and is the mean of Y.
(1)
2.4.2.2. Mutual Information (MI)
An effectual noise-robust correlation value and a nonrandom association between time series can be developed and constructed by mutual information (Khan et al., 2007). To predict MI, we can predict the average number of bits of one of the two time series by expressing the value of the other. Therefore, quantifying the variable X, the average number of the variable Y (i.e. mutual information of the variables X and Y, represented by I(X, Y)) can be predicted by measuring variable X. As a result, we will have MI as (Bonita et al., 2014; Ward & Mazaheri, 2008):
(2)
, and correspondingly designate the number of bins in the variable X’s histogram and the number of components in the variable Y’s histogram, in which does not vitally equal , in general. Besides, the probability that a component in the ith bin of the X axis segregation and the jth bin of the Y axis segregation would respectively constitute an (x, y) pair is the joint probability distribution, i.e. PXY (i,j).
2.4.2.3. Box-Counting Fractal Dimension (BCFD)
In order to predict fractal dimension, we employ self-similarity being conceptualized as the fundamental principle. The equation below is given for the FD of a bounded set A:
(3)
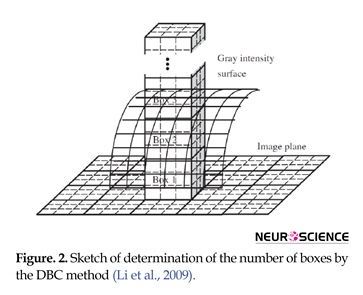
In this regard, the minimum number of A’s discrete copies in the scale r is designated as Nr. We can compute FD just for fractals that are deterministic. Via a box-counting method, a D estimate (i.e. the box-counting DB) can be computed. In the following, we explain the DBC method (Li, Du, & Sun, 2009) . In this case, by plotting each time series of fMRI voxel’s against the other, we are able to create an image of the size M×M (M equals the length of fMRI time series). This image is regarded as a 3D spatial surface, in which the position of pixel on the plane of the image and the gray level of pixel are denoted by (x,y) and (z), the third coordinate. The plane, in this method, is partitioned by the s×s blocks. In each block’s scale (i.e. r=s), s represents an integer and 1 (4)
(i, j)=l−k+1
Additionally, having taken all blocks’ contribution into consideration, is given for the varied measures by:
(5)
Ultimately, the minimum squares linear fit of log (Nr) versus log (l/r) would result in FD being prognosticated.
2.5. Surrogate data
By generating the surrogate data, we aim at evaluating the performance of each method in several pairs of time series, before their applying in the real data. That is because these methods are used as the similarity measure of two time series from two fMRI voxels. We applied the outlined ideas, comparing the total MI, LC and BCFD between the signals in surrogate datasets. These surrogates are generated using the logistic equation (Arora & Santhanam, 2014) and randomization process.
This approach provides us with the opportunity to both test and quantify the deviation from linearity, providing a principled guide in judging the appropriateness of LC, MI and BCFD as measures of FC.
(6)
x(n+1)=A.x(n).(1-x(n))
We exploited logistic equation and increased the A value randomly between 3
2.1. Subjects
A total of 18 normal controls (NCs: 18, aged 23–46 years, mean±SD=31.67±7.98 years, right-handed) were enlisted from the local community. Additionally, we enrolled 17 age-matched methamphetamine-dependent individuals (MDIs: 17 Males, aged 22–39 years, mean±SD=30.52±4.57 years, right-handed). Demographic and clinical information regarding MDIs is demonstrated in Table 1. Mann-Whitney U test (Bergfeldt, Jonsson, Bergfeldt, & Julin, 2015) showed no significant difference between MDIs and NCs (P=0.85).
All subjects were capable to realize and follow the protocol of the study during imaging. Neither MDIs nor NCs had any history of pain, neurologic or psychiatric disorders, head injuries, schizophrenia or an affective disorder, in line with their medical history. The present paper was performed in agreement with the Helsinki Declaration also, confirmed by the Research Ethics Review Board of Tehran University of Medical Sciences in Tehran, Iran. Prior to the MRI scanning, informed written consent was obtained from each subject.
2.2. Data acquisition
On a 3 Tesla Siemens Tim Trio scanner, MRI data were acquired in Medical Imaging Department at Imam Khomeini Hospital, Tehran, Iran. To acquire data for Resting-State Magnetic Resonance Imaging (RS-fMRI), a T2*-weighted gradient-echo Echo-Planar Imaging (EPI) sequence was used with the following parameters: Time of Repetition (TR)=3000 ms, Time of Echo (TE)=30 ms, flip angle=90°, matrix=64×64, field of view (FOV)=192 mm2, thickness/gap=4.5 mm, 22 axial slices covering the whole brain and 240 volumes attained in almost 8 minutes. Besides, via a T1-weighted 3D turbo-gradient-echo sequence (TR=1800 ms, TE=30 ms, flip angle=90°, matrix=256×256, FOV=230×230 mm2, thickness=1.0 mm, and 160 sagittal slices), brain structural images with 3D high resolution were obtained. The participants were supposed to have their eyes closed, keep calm, not to systematically think about anything, and not to fall asleep. None of the lights in the scanner room were on during the RS-fMRI scanning.
2.3. Data preprocessing
All the fMRI data were preprocessed using MATLAB software and DPARSF_V2.0 Toolbox (Chao-Gan & Yu-Feng, 2010). For each individual, in the first place, the first 10 volume images were excluded from the RS-fMRI data to make the subjects adapt to the environment and to stabilize the scanner, letting 260 volumes remain for supplementary analysis. Then, to correct the acquisition time delay between slices within the similar TR, slice timing was administered. After that, for the correction of the inter-TR head motions, realignment to the first volume was done. Next, we spatially normalized the fMRI data to a standard Montreal Neurological Institute (MNI) (Tzourio-Mazoyer et al., 2002) template and implemented resampling to a voxel size of 36×63 mm3. According to the studies conducted so far, no spatial smoothing was applied (Achard & Bullmore, 2007; Braun et al., 2012; Wang et al., 2009). Eventually, to reduce the low-frequency drift and high-frequency physiological noise, band-pass filtering was performed for each voxel at the frequency of 0.01–0.08 Hz. The RS-fMRI data for each subject were checked for head motion. In accord with the criteria that the translation and rotation of head motion in any direction were not more than 1.5 mm or 1.5, none of the subjects were disqualified.
2.4. Graph construction
Topological properties of the brain were investigated through the method of binary graph G=(V, E), where a brain region (i.e. ROI) and an edge (E) between two nodes in the graph are indicated by a node/vertex (V). All the regarded graphs in this work are undirected. To analyze complex network, we applied a simple generalization of the graph called weighted graph (Bollobás, 1998).
In this paper, based on the previously conducted studies, two common methods (i.e. LC (Hlinka et al., 2011)and MI (Hartman, Hlinka, Paluš, Mantini, & Corbetta, 2011)), as well as the proposed method (i.e. BCFD) were applied for edge definition. For graph construction, node and edge need to be defined, each of which is explained in detail as follows:
2.4.1. Node definition
In order to have the brain parcellated into 90 Regions Of Interest (ROIs) (45 in each hemisphere), an Automated Anatomical Labeling (AAL) atlas (Tzourio-Mazoyer et al., 2002) was utilized to construct the brain functional networks for each participant.
2.4.2. Edge definition
At this stage, the connectivity, dependence and interactions between the brain regions, i.e. the graph nodes, have to be quantified. Edge definition phase to create graph functional connectivity is challenging to some extent, for which various methods, including linear and nonlinear are presented so far (Ahmadlou & Adeli, 2011; Ahmadlou, Ahmadi, Rezazade, & Azad-Marzabadi, 2013). It should be noted that the method considered as the best method for edge definition and as the edge definition gold standard is still a questionable issue (Papo et al., 2014). According to the previous studies, we used LC and MI methods as the representatives of the linear and non-linear methods, respectively, together with the proposed method “BCFD” for quantifying the interactions between 90 regions selected as nodes based on AAL Atlas. Then, BCFD method was evaluated in comparison with LC and MI. To quantify the nodes connectivity, each of these three methods considers a different criterion.
LC method quantifies the interactions between the time series of each node with linearity supposition, while MI lacks the assumption of the linearity between the brain regions and proposes an index for the evaluation of the shared information between the two time series. But this method is sensitive to the length of time series being analyzed. Since, in functional connectivity studies, the length of time series is usually short, MI use can be somewhat challenging. BCFD was applied in the current study, as it is based on the concept of self-similarity and complexity, i.e. distribution of the points in the phase space, calculating the connectivity and interactions of the brain regions. In addition, it does not assume interactions linearity or sensitive to the length of the time series. The concepts of “self-similarity” and “complexity” have not been evaluated using the graph theory in the functional connectivity studies. We computed the time series for each ROI, by averaging the signals of all voxels within that region. By calculating the Pearson correlation coefficient, MI and BCFD in the residual time courses between all ROI-pairs, a 90×90 adjacency matrix was attained for each subject.
2.4.2.1. Pearson correlation coefficient
A value for the linear association between the time series to be quantified is Pearson correlation, by which the dependence structure Gaussianity presupposition is given. Regarding {X}={x1,x2,xND} and {Y}={y1,y2,yND} as the voxel’s time series, the number of components in each set would be. You will get the Pearson correlation coefficient r as the following equation (Gómez, Vaquero, López-Mendoza, González-Rosa, & Vázquez-Marrufo, 2004) in which is the mean of X and is the mean of Y.
(1)
2.4.2.2. Mutual Information (MI)
An effectual noise-robust correlation value and a nonrandom association between time series can be developed and constructed by mutual information (Khan et al., 2007). To predict MI, we can predict the average number of bits of one of the two time series by expressing the value of the other. Therefore, quantifying the variable X, the average number of the variable Y (i.e. mutual information of the variables X and Y, represented by I(X, Y)) can be predicted by measuring variable X. As a result, we will have MI as (Bonita et al., 2014; Ward & Mazaheri, 2008):
(2)
, and correspondingly designate the number of bins in the variable X’s histogram and the number of components in the variable Y’s histogram, in which does not vitally equal , in general. Besides, the probability that a component in the ith bin of the X axis segregation and the jth bin of the Y axis segregation would respectively constitute an (x, y) pair is the joint probability distribution, i.e. PXY (i,j).
2.4.2.3. Box-Counting Fractal Dimension (BCFD)
In order to predict fractal dimension, we employ self-similarity being conceptualized as the fundamental principle. The equation below is given for the FD of a bounded set A:
(3)
In this regard, the minimum number of A’s discrete copies in the scale r is designated as Nr. We can compute FD just for fractals that are deterministic. Via a box-counting method, a D estimate (i.e. the box-counting DB) can be computed. In the following, we explain the DBC method (Li, Du, & Sun, 2009) . In this case, by plotting each time series of fMRI voxel’s against the other, we are able to create an image of the size M×M (M equals the length of fMRI time series). This image is regarded as a 3D spatial surface, in which the position of pixel on the plane of the image and the gray level of pixel are denoted by (x,y) and (z), the third coordinate. The plane, in this method, is partitioned by the s×s blocks. In each block’s scale (i.e. r=s), s represents an integer and 1
(i, j)=l−k+1
Additionally, having taken all blocks’ contribution into consideration, is given for the varied measures by:
(5)
Ultimately, the minimum squares linear fit of log (Nr) versus log (l/r) would result in FD being prognosticated.
2.5. Surrogate data
By generating the surrogate data, we aim at evaluating the performance of each method in several pairs of time series, before their applying in the real data. That is because these methods are used as the similarity measure of two time series from two fMRI voxels. We applied the outlined ideas, comparing the total MI, LC and BCFD between the signals in surrogate datasets. These surrogates are generated using the logistic equation (Arora & Santhanam, 2014) and randomization process.
This approach provides us with the opportunity to both test and quantify the deviation from linearity, providing a principled guide in judging the appropriateness of LC, MI and BCFD as measures of FC.
(6)
x(n+1)=A.x(n).(1-x(n))
We exploited logistic equation and increased the A value randomly between 3
2.6. Thresholding method
Presently, for studies on complex brain network, there is no consensus over selection of a specified threshold (Achard & Bullmore, 2007). Pursuant to studies already carried out, each element’s absolute value (positive and negative values were only contained in Pearson’s matrix) was applied as the inter-regional functional connectivity (Bassett et al., 2008; Braun et al., 2012; Wang et al., 2011; Zhang et al., 2011). Ultimately, we thresholded these matrices of adjacency into a binary matrix.
In this study, for the networks properties to be investigated, we employed a range of threshold values, from 0.1 to 0.5, with an increment of 0.1. In this method to derive adjacency matrices, we thresholded them in a proportional manner (i.e. normalization by “wiring cost” – e.g. 0.1 represents 10% of the strongest connections being maintained as links). For each individual, a connectivity matrix of 90×90 was obtained and the topological organization of functional networks of the whole brain analyzed in compliance with graph theory, taking each ROI into account as a node and the functional connectivity as an edge.
2.7. Topological properties of brain networks
Of all the multiple matrices of network we needed to measure for the assessment of the small-world properties (Sporns & Zwi, 2004), the Clustering Coefficient (CC) and the mean minimum Path Length (PL) are regarded to be the major components of the small-world network. The clustering coefficient ratio, 0˂CCi˂1, describes the range or amount of potential connections that the closest neighbors of a node actually has (Liu et al., 2009):
(7)
The total number of nodes of a network, the number of edges by which node j’s neighbors are connected to one another and the number of node j’s neighbors are illustrated by N, #Ej and #Vj in this equation, correspondingly. Moreover, we will have L (i.e. the minimum path length), dividing the shortest path lengths in average by each potential vertices pair:
(8)
In the above formula, the path length is determined by the number of edges the path encompasses. Also delineates the shortest length (i.e. the ith or the jth). The average minimum number of connections linking any two nodes of the network is referred to as the Characteristic Path Length (CPL). Furthermore, we computed, for a CC and CPL graph containing as many nodes as edges, the corresponding parameters, according to what and determine. These random networks were established to obliterate any structure of local adjacency, when the primary level of distribution is kept. This was carried out by each edge being reattached in the original network, 1000 times in average, randomly (Hayasaka & Laurienti, 2010; Newman, Strogatz, & Watts, 2001). Random networks require a shortest path length in average which is small, having limited local interconnections resulting in a small Crand and Lrand. The graph, on the ground that it has a small shortest length in average and its average clustering coefficient is strikingly greater than a constructed random graph on the same number of nodes, would be regarded as small-world. It has been demonstrated that, supporting effective parallel transmission of information at a comparatively low cost, economical small-world properties with high global efficiency (Eglobal) are owned by the brain functional networks. The harmonic mean inverse of the least absolute path length between each nodes pair, is delineated as (Liu et al., 2008).
(9)
For two groups of addicts and normal individuals, clustering coefficient, characteristic path length and efficiency were computed for edge definition using the three methods of LC, MI and BCFD, respectively. It should be noted that the nature of the graphs obtained by these three methods is different to some extent, where LC method quantifies the linear interactions between the nodes, MI calculates the shared information and BCFD computes the self-similarity. Thus, the values of clustering coefficient, path length and efficiency in the graphs obtained by LC and MI and BCFD methods will be different. But, regardless of the nature of these three graphs and the varied values of the features, the interpretation of clustering coefficient, path length and efficiency will be the same in all three graphs.
2.8. Statistical analysis
To evaluate the brain network properties, statistical difference between addict participants and normal controls, a test of non-parametric permutation was applied (He, Chen, & Evans, 2008). In the first place, we calculated the network topological properties inclusive of Clustering Coefficients, Characteristic Path Length (CPL) and Global Efficiency (GE). Next, each individual’s regional cortical thickness measures were assigned to either group randomly. In addition, we recomputed LC, MI and BCFD matrices for each of the 2 groups randomized and, for the network property measure, obtained a new value. We repeated this process of randomization 1000 times. Because less than 5 percentile of intergroup difference in the distribution of permutation is more than the discrepancy in the observed group, the significance would be reached. For each threshold, the procedure was repeated.
3. Result
Investigated from a functional integration viewpoint and in line with LC, MI and BCFD methods, methamphetamine addiction problems were considered through graph topological properties. In order for the network to be built, for both methamphetamine users and normal controls, graph theory was applied, enabling us to analyze the topological properties of functional brain networks between these two groups.
By generating the surrogate data, we aim at evaluating the performance of each method in several pairs of time series, before they are applied for the real data. That is because these methods are used as the similarity measure of two time series from two fMRI voxels. These similarity measures are compared and assessed using the time series with linear and non-linear behavior, about which we have prior knowledge. To evaluate LC, MI and BCFD methods, two surrogate data sets generated by the randomization process (as linear behavior) and by the logistic equation (as a non-linear behavior) were used.
Figure 3 shows the results of creating six time series using logistic equation. Upper signals correspond to less nonlinearity and more linearity and lower signals correspond to more nonlinearity and less linearity. As can be seen, there are a few similarities in the signals. We aim at quantifying these similarities using BCFD and evaluating the results of BCFD versus LC and MI.
As seen in Figure 3, with an increase in the value of A in logistic equation, complexity increases, interpreted based on an increase in the distribution of points in the phase space, while the similarity and connectivity of the two time series decrease in a non-linear manner. For these six typical time series (3 pairs), linear correlation, mutual information and box counting were executed and the similarity measures were computed. Table 2 displays the results.
As seen in Table 2 and based on the visual comparison, by increasing nonlinearity, LC has no significant changes in the values of these three methods for nonlinear range and just has a good performance in linear range, MI has an increasing trend representing that mutual information functions well just in nonlinear range. Among these three algorithms only BCFD has significant changes and shows the capability of its discrimination for similarity measure in both linear and nonlinear ranges.
Based on our statistical analysis using BCFD and consistent with several previously conducted studies on addiction, there was a significant difference between groups in global efficiency, clustering coefficient, as well as Characteristic Path Length (CPL) at different thresholds (Ersche et al., 2006; Jiang et al., 2013).
Graph topological properties of both addict subjects and normal controls using MI method is presented in Figure 6a, Figure 6b and Figure 6c. In this respect, similar to the analysis using LC, significant differences at a number of network thresholds for CC, CPL and GE (red circles, P<0.05) were revealed. Conforming to the results, as compared to those of addict subjects, relatively higher CC and GE were exhibited by the networks of normal controls. Furthermore, implying that MI is more robust than LC to extract to the differences in graph topological features, the number of significant differences using MI is more than those through LC method.
Figure 7 illustrates the statistical analysis of the graph topological properties using BCFD. Once more, identical to the analysis utilizing LC and MI, as compared with normal controls, brain networks of addicted participants display significant differences in CC, CPL and
4. Discussion
A prominent approach to the analysis of fMRI data, in particular the resting state data is Functional Connectivity (FC). Two common methods of functional connectivity analysis are graph theory and seed-based analysis which employ Linear Correlation (LC) measures. An implicit assumption of Gaussianity is applied to the dependence structure by utilizing linear correlation measures (Chang & Glover, 2010). It is of a great importance to bear in mind that non-Gaussianity may result in the false detection of nonstationarity. It should also be kept in mind that, rather than with neuronal activations, we are dealing with the level of fMRI BOLD signal; the non-neural sources of variation are likely to influence, to some extent, the contributions of both the Gaussian and non-Gaussian. Due to generality, a specific position is held by Mutual Information (MI) among a great number of possible nonlinear FC measure candidates. Theoretically, adopting an arbitrary form of dependence association among the variables, without any apriority model limitations on its form, would be general enough. MI features provide us with the opportunity not only to examine the appropriateness of linear correlation for fMRI time series, but also to quantify the information disregarded using linear correlation. Owing to greater sensitivity of MI to higher order statistics considering only the second order (Smith et al., 2011), as compared to LC, an extra amount of information is resulted and the possible contribution of non-linear alternatives over the Pearson correlation coefficient is bounded.
Currently by employing the elements of chaos theory, modern neuroscientists have been able to recognize the fractal properties present in the brain functions (Expert et al., 2011; Papo et al., 2014; You & Stadler, 2012). However, until just the recent time, there was no analytical method for the objective explanation of the brain complexity. However, the question of which interdependence or connectivity measures to be applied is not generally responded. The crucial trade-off factors would probably depend upon a specific dataset and the regarding scientific problem (Hartman et al., 2011).
The surrogate data analysis conducted applying the logistic equation may give us the insight to fractal behavior impact on the brain complex networks. Figure 8 displays the performance of these 3 algorithms with increasing the complexity. As desired, correlation has a good performance in only linear range because of its fluctuation. MI has a good performance in only nonlinear, but BCFD performs well in both linear and nonlinear ranges, expressing that BFCD is a better dependency measure for
In order to better evaluate the similarity measures applied in the brain functional connectivity using the graph theory, other surrogate data were created using the randomization process. In these data, as shown in Figure 9, in the first step where the two signals are completely similar to one another, their values have to be the maximum value. Since in establishing the random signal pairs, the trend is a monotonic downward trend, the values of similarity measures have to lack fluctuations. The last important point is that, in the last stage, the similarity of the pair of signals would be a specific number; hence, in the last phase, similarity measures should have a value similar to that specific value.
As seen in Figure 9, all the three similarity measures are started from the maximum value, which seems reasonable, knowing that two signal pairs are completely similar. However, compared to the other methods, the Linear Correlation (LC) has more fluctuations, which is not desirable due to less similarity of each signal pair in proportion to the prior signal pair in the surrogate data. In spite of its lower fluctuations, Mutual Information (MI) method does not perform greatly for low similarity values. That is because, in the last stages where the specific value of 30% in the surrogate data, for example, has been already given to the similarity, a much higher value is shown by the use of this measure. Among the similarity measures, Box-Counting Fractal Dimension (BCFD) seems to have been able to follow all the existent behavior, and thus, it can have a better performance for the graph edge determination in brain functional connectivity analyses.
By reducing the similarity value, LC method has a great number of fluctuations and MI follows the variations in the similarity reduction with a very little slope, whereas FD follows the variations in the similarity reduction well. Being repeated 1000 times, the results from the statistical analysis showed no significant difference between LC, MI and FD methods in the data generated through randomization. Similar to the randomization method, we reduce the similarity of the time series to one another in a linear manner, such a conclusion seems reasonable. That is because, in fact, the data still have a linear relationship with each other. However, in the data created by the logistic equation, a significant difference was observed between the three methods. Similarly, this result is not far-fetched, as with an increase in the value of A in the logistic equation, complexity (distribution of points in the phase space), i.e. the non-linear interaction between the time series will increase. Regarding the evidence cited in the surrogate data, it can be concluded that FD seems to be a more appropriate criterion for the graph edge determination in functional connectivity studies.
There is a number of well-established circuits characterizing the cognitive impairments of addicted brain; namely decision-making, impulsivity, attention disturbances and assigning emotional valence circuits (Lee & Pau, 2002; Lee et al., 2005; Li & Sinha, 2008; Volkow, Fowler, & Wang, 2003). Studies have also suggested some irregularities in these circuits for methamphetamine dependents (Monterosso, Aron, Cordova, Xu, & London, 2005). To this end, studying these circuits in MDI through a graph theoretical perspective is beneficial. In the current study, alterations were found in MDIs universal parameters of the brain functional networks, in comparison with those of NCs. Statistical analysis revealed a significant decrease in clustering coefficient, global efficiency and small-world indices and increase in characteristic path length of MDIs.
One of the indices characterizing the manner in which the brain networks are shifted to either a regular or a random network is the clustering coefficient (He & Evans, 2010). Studies have previously shown a decreased clustering coefficient in ADHD individuals justifying their attention disorders (Wang, Li, Metzak, He, & Woodward, 2010), this may also be the case for our MDIs as attention deficit is a commonly reported cognitive impairment in meth addiction (Sim et al., 2001).
Universal processing and transfer of information from each brain region to all the other ones is taken into consideration by global efficiency, which, to ensure effective interactions or rapid information transfer over the distant cortical regions involved in the basis of a great number of cognitive processes, predominantly relates the long-range connections (Latora & Marchiori, 2001). Low global efficiency is linked to lower IQ score (Li et al., 2009; Van den Heuvel, Stam, Kahn, & Pol, 2009), which may be due to a slower information process, a critical subscale in IQ score; consistently lower global efficiency can be indicative of decreased information process speed in MDIs.
The mean minimum number of links connecting any two nodes within the network is considered as the characteristic path length of a network. Giving an overview of information transfer effectiveness and measuring the functional integration of the whole brain, the capability for the brain network parallel information propagation is quantified by the characteristic path length of a network (Tschernegg et al., 2013). Obviously, a longer characteristic path length will make for a more time consuming and/or less efficient integration of modules. Increase in characteristic path length in our participants can be a reason for the observed psychomotor retardation of brain functions in abstinent psycho stimulant-dependent individuals (Pulvirenti & Koob, 1993).
The model of small-world network topology is considered by a high local clustering coefficient and shortest path length (Rubinov & Sporns, 2010). Small-world properties lead to maintaining highly effective, specialized modular information process and fast global information transfer in a network (Kaiser & Hilgetag, 2006). Similar to earlier studies on functional networks of the human brain (Liao et al., 2010; Liu et al., 2008; Supekar et al., 2008; Tian, Wang, Yan, & He, 2011; Zhang et al., 2011), in this study, the small-world properties of MDIs’ and NCs’ resting networks were investigated over a range of threshold values. Statistical comparison of the two groups showed that small-world properties were conserved by both MDIs’ and NCs’ whole-brain functional network. The small-world scalar was smaller in MDIs than the NCs (Figure 10). Small-word property increases through brain development, representing a shift of brain networks towards regularity (Park et al., 2015); indicating improved decision making in adults. Inversely, low small-world scalar in our study may be a reason for common cognitive impairments in MDIs, especially disrupted decision making (Kohno, Morales, Ghahremani, Hellemann, & London, 2014) and impulsive behaviors, a hint of a shift towards randomness.
By comparing the edge definition methods and the features derived from functional connectivity graph, it is concluded that there is a significant difference in the brain network topological features of the addicts, compared to those of the control group; in all three edge definition methods, the difference was obtained in terms of network topological features. The number of significant points, however, are more in BCFD method than in LC and even MI. As stated in Liu et al. study (Liu et al., 2009), the greater number of significant points, regardless of the connectivity threshold, can be a criterion for the comparison of these methods. These materials can certify the proof of the main and sub-hypotheses of this research.
According to the gathered body of evidence, a more powerful manner to appreciate the brain networks topological principles is put up by the graph theoretical analysis of neuroimaging data applying BCFD than through LC and MI methods. Using resting-state fMRI and a graph theory method, we aimed at investigating the functional network of the whole-brain in MDIs. As lower clustering coefficient, global efficiency and lessened small-worldness indicate, the whole-brain functional networks in MDIs, compared to those in normal controls, were pointed out to be probably shifted toward random organization.
On the whole, the present study found disruptions in the whole-brain functional networks topological graph properties of MDIs. The findings are valuable to better understand the underlying mechanisms of addiction. Due to such efforts, recently developed research areas of interest to all basic scientists and clinical researchers are being opened up into organizational mechanisms of the brain. Considering the features of graph theory in establishment of network alterations, it seems to be a suitable biomarker for monitoring addiction treatment and detecting the treatment progress ahead of significant clinical symptoms.
Acknowledgements
This study has been financially supported by Tehran University of Medical Sciences (Grant No: 20125).
Conflict of Interest
All authors certify that this manuscript has neither been published in whole nor in part nor being considered for publication elsewhere. The authors have no conflicts of interest to declare.
References
Achard, S., & Bullmore, E. (2007). Efficiency and cost of economical brain functional networks. PLoS Computational Biology, 3(2), 17. doi: 10.1371/journal.pcbi.0030017
Ahmadi, K., Ahmadlou, M., Rezazade, M., Azad-Marzabadi, E., & Sajedi, F. (2013). Brain activity of women is more fractal than men. Neuroscience Letters, 535, 7-11. doi: /10.1016/j.neulet.2012.12.043
Ahmadlou, M., & Adeli, H. (2011). Functional community analysis of brain: a new approach for EEG-based investigation of the brain pathology. Neuroimage, 58(2), 401-408. doi: 10.1016/j.neuroimage.2011.04.070
Ahmadlou, M., Ahmadi, K., Rezazade, M., & Azad-Marzabadi, E. (2013). Global organization of functional brain connectivity in methamphetamine abusers. Clinical Neurophysiology, 124(6), 1122-31. doi: 10.1016/j.clinph.2012.12.003
Arora, S., & Santhanam, M. (2014). Synchronization of coupled map lattice using delayed variable feedback. Journal of Applied Nonlinear Dynamics, 3(3), 245-53. doi: 10.5890/jand.2014.09.004
Bassett, D. S., Bullmore, E., Verchinski, B. A., Mattay, V. S., Weinberger, D. R., & Meyer-Lindenberg, A. (2008). Hierarchical organization of human cortical networks in health and schizophrenia. Journal of Neuroscience, 28(37), 9239-48. doi: 10.1523/jneurosci.1929-08.2008
Bassett, D. S., & Bullmore, E. T. (2009). Human brain networks in health and disease. Current Opinion in Neurology, 22(4), 340-47. doi: 10.1097/wco.0b013e32832d93dd
Bergfeldt, U., Jonsson, T., Bergfeldt, L., & Julin, P. (2015). Cortical activation changes and improved motor function in stroke patients after focal spasticity therapy–an interventional study applying repeated fMRI. BMC Neurology, 15(1), 52. doi: 10.1186/s12883-015-0306-4
Bollobás, B. (1998). Modern graph theory (Vol. 184). Berlin: Springer Science & Business Media.
Bonita, J., Ambolode II, L., Rosenberg, B., Cellucci, C., Watanabe, T., Rapp, P., et al. (2014). Time domain measures of inter-channel EEG correlations: A comparison of linear, nonparametric and nonlinear measures. Cognitive Neurodynamics, 8(1), 1-15. doi: 10.1007/s11571-013-9267-8
Braun, U., Plichta, M. M., Esslinger, C., Sauer, C., Haddad, L., Grimm, O., et al. (2012). Test–retest reliability of resting-state connectivity network characteristics using fMRI and graph theoretical measures. Neuroimage, 59(2), 1404-12. doi: 10.1016/j.neuroimage.2011.08.044
Bullmore, E., & Sporns, O. (2009). Complex brain networks: graph theoretical analysis of structural and functional systems. Nature Reviews Neuroscience, 10(3), 186-198. doi: 10.1038/nrn2575
Cabral, J., Kringelbach, M., & Deco, G. (2012). Functional graph alterations in schizophrenia: A result from a global anatomic decoupling? Pharmacopsychiatry, 45(S01), S57-S64. doi: 10.1055/s-0032-1309001
Chang, C., & Glover, G. H. (2010). Time–frequency dynamics of resting-state brain connectivity measured with fMRI. Neuroimage, 50(1), 81-98. doi: 10.1016/j.neuroimage.2009.12.011
Chao-Gan, Y., & Yu-Feng, Z. (2010). DPARSF: A MATLAB toolbox for “pipeline” data analysis of resting-state fMRI. Frontiers in System Neuroscience, 4. doi: 10.3389/fnsys.2010.00013
Culham, J. C., & Kanwisher, N. G. (2001). Neuroimaging of cognitive functions in human parietal cortex. Current Opinion in Neurobiology, 11(2), 157-163. doi: 10.1016/s0959-4388(00)00191-4
Deuker, L., Bullmore, E. T., Smith, M., Christensen, S., Nathan, P. J., Rockstroh, B., et al. (2009). Reproducibility of graph metrics of human brain functional networks. Neuroimage, 47(4), 1460-68. doi: 10.1016/j.neuroimage.2009.05.035
Donges, J. F., Zou, Y., Marwan, N., & Kurths, J. (2009). Complex networks in climate dynamics. The European Physical Journal Special Topics, 174(1), 157-179. doi: 10.1140/epjst/e2009-01098-2
Ersche, K. D., Fletcher, P. C., Roiser, J. P., Fryer, T. D., London, M., Robbins, T. W., et al. (2006). Differences in orbitofrontal activation during decision-making between methadone-maintained opiate users, heroin users and healthy volunteers. Psychopharmacology, 188(3), 364-373. doi: 10.1007/s00213-006-0515-z
Expert, P., Lambiotte, R., Chialvo, D. R., Christensen, K., Jensen, H. J., Sharp, D. J., et al. (2011). Self-similar correlation function in brain resting-state functional magnetic resonance imaging. Journal of The Royal Society Interface, 8(57), 472-479. doi: 10.1098/rsif.2010.0416
Fransson, P. (2005). Spontaneous low‐frequency BOLD signal fluctuations: An fMRI investigation of the resting‐state default mode of brain function hypothesis. Human Brain Mapping, 26(1), 15-29. doi: 10.1002/hbm.20113
Gómez, C. M., Vaquero, E., López-Mendoza, D., González-Rosa, J., & Vázquez-Marrufo, M. (2004). Reduction of EEG power during expectancy periods in humans. Acta Neurobiologiae Experimentalis, 64(2), 143-51. PMID: 15366247
Hartman, D., Hlinka, J., Paluš, M., Mantini, D., & Corbetta, M. (2011). The role of nonlinearity in computing graph-theoretical properties of resting-state functional magnetic resonance imaging brain networks. Chaos: An Interdisciplinary Journal of Nonlinear Science, 21(1), 013119. doi: 10.1063/1.3553181
Hayasaka, S., & Laurienti, P. J. (2010). Comparison of characteristics between region-and voxel-based network analyses in resting-state fMRI data. Neuroimage, 50(2), 499-508. doi: 10.1016/j.neuroimage.2009.12.051
He, Y., Chen, Z., & Evans, A. (2008). Structural insights into aberrant topological patterns of large-scale cortical networks in Alzheimer’s disease. Journal of Neuroscience, 28(18), 4756-66. doi: 10.1523/jneurosci.0141-08.2008
He, Y., & Evans, A. (2010). Graph theoretical modeling of brain connectivity. Current Opinion in Neurology, 23(4), 341-350. doi: 10.1097/wco.0b013e32833aa567
Hlinka, J., Paluš, M., Vejmelka, M., Mantini, D., & Corbetta, M. (2011). Functional connectivity in resting-state fMRI: is linear correlation sufficient? Neuroimage, 54(3), 2218-25. doi: 10.1016/j.neuroimage.2010.08.042
Jiang, G., Wen, X., Qiu, Y., Zhang, R., Wang, J., Li, M., et al. (2013). Disrupted topological organization in whole-brain functional networks of heroin-dependent individuals: A resting-state FMRI study. PLoS ONE, 8(12), e82715. doi: 10.1371/journal.pone.0082715
Kaiser, M., & Hilgetag, C. C. (2006). Nonoptimal component placement, but short processing paths, due to long-distance projections in neural systems. PLoS Computational Biology, 2(7), e95. doi: 10.1371/journal.pcbi.0020095
Khan, S., Bandyopadhyay, S., Ganguly, A. R., Saigal, S., Erickson III, D. J., Protopopescu, V., et al. (2007). Relative performance of mutual information estimation methods for quantifying the dependence among short and noisy data. Physical Review E, 76(2), 026209. doi: 10.1103/physreve.76.026209
Kohno, M., Morales, A. M., Ghahremani, D. G., Hellemann, G., & London, E. D. (2014). Risky decision making, prefrontal cortex, and mesocorticolimbic functional connectivity in methamphetamine dependence. JAMA psychiatry, 71(7), 812-820. doi: 10.1001/jamapsychiatry.2014.399
Kreuz, T., Mormann, F., Andrzejak, R. G., Kraskov, A., Lehnertz, K., & Grassberger, P. (2007). Measuring synchronization in coupled model systems: A comparison of different approaches. Physica D: Nonlinear Phenomena, 225(1), 29-42. doi: 10.1016/j.physd.2006.09.039
Latora, V., & Marchiori, M. (2001). Efficient behavior of small-world networks. Physical Review Letters, 87(19), 198701. doi: 10.1103/physrevlett.87.198701
Lee, T. M., & Pau, C. W. (2002). Impulse control differences between abstinent heroin users and matched controls. Brain Injury, 16(10), 885-89. doi: 10.1080/02699050210128915
Lee, T. M., Zhou, W. H., Luo, X. J., Yuen, K. S., Ruan, X. Z., & Weng, X. C. (2005). Neural activity associated with cognitive regulation in heroin users: A fMRI study. Neuroscience Letters, 382(3), 211-216. doi: 10.1016/j.neulet.2005.03.053
Li, C. S. R., & Sinha, R. (2008). Inhibitory control and emotional stress regulation: neuroimaging evidence for frontal–limbic dysfunction in psycho-stimulant addiction. Neuroscience & Biobehavioral Reviews, 32(3), 581-597. doi: 10.1016/j.neubiorev.2007.10.003
Li, J., Du, Q., & Sun, C. (2009). An improved box-counting method for image fractal dimension estimation. Pattern Recognition, 42(11), 2460-69. doi: 10.1016/j.patcog.2009.03.001
Li, Y., Liu, Y., Li, J., Qin, W., Li, K., Yu, C., et al. (2009). Brain anatomical network and intelligence. PLoS Computational Biology, 5(5), e1000395. doi: 10.1371/journal.pcbi.1000395
Liao, W., Zhang, Z., Pan, Z., Mantini, D., Ding, J., Duan, X., et al. (2010). Altered functional connectivity and small-world in mesial temporal lobe epilepsy. PLoS ONE, 5(1), e8525. doi: 10.1371/journal.pone.0008525
Liu, J., Liang, J., Qin, W., Tian, J., Yuan, K., Bai, L., et al. (2009). Dysfunctional connectivity patterns in chronic heroin users: An fMRI study. Neuroscience Letters, 460(1), 72-77. doi: 10.1016/j.neulet.2009.05.038
Liu, Y., Liang, M., Zhou, Y., He, Y., Hao, Y., Song, M., et al. (2008). Disrupted small-world networks in schizophrenia. Brain, 131(4), 945-961. doi: 10.1093/brain/awn018
Mamashli, F., Ahmadlu, M., Golpayegani, M. R., Gharibzadeh, S. (2010). Detection of attention using chaotic global features. Journal of Neuropsychiatry and Clinical Neurosciences, 22(2), E20. doi: 10.1176/jnp.2010.22.2.247.e20
Monterosso, J. R., Aron, A. R., Cordova, X., Xu, J., & London, E. D. (2005). Deficits in response inhibition associated with chronic methamphetamine abuse. Drug and Alcohol Dependence, 79(2), 273-77. doi: 10.1016/j.drugalcdep.2005.02.002
Nakamura, T., Hillary, F. G., & Biswal, B. B. (2009). Resting network plasticity following brain injury. PLoS ONE, 4(12), e8220. doi: 10.1371/journal.pone.0008220
Newman, M. E., Strogatz, S. H., & Watts, D. J. (2001). Random graphs with arbitrary degree distributions and their applications. Physical Review E, 64(2), 026118. doi: 10.1103/physreve.64.026118
Papo, D., Zanin, M., & Buldú, J. M. (2014). Reconstructing functional brain networks: Have we got the basics right? Frontiers in Human Neuroscience, 8. doi: 10.3389/fnhum.2014.00107
Park, C. h., Chun, J. W., Cho, H., Jung, Y. C., Choi, J., & Kim, D. J. (2015). Is the Internet gaming‐addicted brain close to be in a pathological state? Addiction Biology, 22(1), 196-205. doi: 10.1111/adb.12282
Ponten, S., Bartolomei, F., & Stam, C. (2007). Small-world networks and epilepsy: Graph theoretical analysis of intracerebrally recorded mesial temporal lobe seizures. Clinical Neurophysiology, 118(4), 918-27. doi: 10.1016/j.clinph.2006.12.002
Pulvirenti, L., & Koob, G. F. (1993). Lisuride reduces psychomotor retardation during withdrawal from chronic intravenous amphetamine self-administration in rats. Neuropsychopharmacology, 8(3), 213-18. doi: 10.1038/npp.1993.23
Rubinov, M., & Sporns, O. (2010). Complex network measures of brain connectivity: Uses and interpretations. Neuroimage, 52(3), 1059-69. doi: 10.1016/j.neuroimage.2009.10.003
Sim, T., Simon, S. L., Domier, C. P., Richardson, K., Rawson, R. A., & Ling, W. (2001). Cognitive deficits among methamphetamine users with attention deficit hyperactivity disorder symptomatology. Journal of Addictive Diseases, 21(1), 75-89. doi: 10.1300/j069v21n01_07
Smith, S. M., Matthews, P. M., & Jezzard, P. (2001). Functional MRI: An introduction to methods. Oxford: Oxford University Press.
Smith, S. M., Miller, K. L., Salimi-Khorshidi, G., Webster, M., Beckmann, C. F., Nichols, T. E., et al. (2011). Network modelling methods for FMRI. Neuroimage, 54(2), 875-891. doi: 10.1016/j.neuroimage.2010.08.063
Sporns, O. (2006). Small-world connectivity, motif composition, and complexity of fractal neuronal connections. Biosystems, 85(1), 55-64. doi: 10.1016/j.biosystems.2006.02.008
Sporns, O., & Zwi, J. D. (2004). The small world of the cerebral cortex. Neuroinformatics, 2(2), 145-162. doi: doi.org/10.1385/ni:2:2:145
Sun, J., Tong, S., & Yang, G. Y. (2012). Reorganization of brain networks in aging and age-related diseases. Aging and disease, 3(2), 181-93. PMID: 22724079
Supekar, K., Menon, V., Rubin, D., Musen, M., & Greicius, M. D. (2008). Network analysis of intrinsic functional brain connectivity in Alzheimer’s disease. PLoS Computational Biology, 4(6), e1000100. doi: 10.1371/journal.pcbi.1000100
Sutherland, M. T., McHugh, M. J., Pariyadath, V., & Stein, E. A. (2012). Resting state functional connectivity in addiction: Lessons learned and a road ahead. Neuroimage, 62(4), 2281-95. doi: 10.1016/j.neuroimage.2012.01.117
Tian, L., Wang, J., Yan, C., & He, Y. (2011). Hemisphere-and gender-related differences in small-world brain networks: A resting-state functional MRI study. Neuroimage, 54(1), 191-202. doi: 10.1016/j.neuroimage.2010.07.066
Tschernegg, M., Crone, J. S., Eigenberger, T., Schwartenbeck, P., Fauth-Bühler, M., Lemènager, T., et al. (2013). Abnormalities of functional brain networks in pathological gambling: A graph-theoretical approach. Frontiers in Human Neuroscience, 7. doi: 10.3389/fnhum.2013.00625
Tzourio-Mazoyer, N., Landeau, B., Papathanassiou, D., Crivello, F., Etard, O., Delcroix, N., et al. (2002). Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage, 15(1), 273-89. doi: 10.1006/nimg.2001.0978
Van den Heuvel, M. P., Stam, C. J., Kahn, R. S., & Pol, H. E. H. (2009). Efficiency of functional brain networks and intellectual performance. Journal of Neuroscience, 29(23), 7619-24. doi: 10.1523/jneurosci.1443-09.2009
Volkow, N. D., Fowler, J. S., & Wang, G. J. (2003). The addicted human brain: Insights from imaging studies. Journal of Clinical Investigation, 111(10), 1444-51. doi: 10.1172/jci200318533
Wang, J. H., Zuo, X. N., Gohel, S., Milham, M. P., Biswal, B. B., & He, Y. (2011). Graph theoretical analysis of functional brain networks: test-retest evaluation on short-and long-term resting-state functional MRI data. PLoS ONE, 6(7), e21976. doi: 10.1371/journal.pone.0021976
Wang, J., Wang, L., Zang, Y., Yang, H., Tang, H., Gong, Q., et al. (2009). Parcellation‐dependent small‐world brain functional networks: A resting‐state fMRI study. Human Brain Mapping, 30(5), 1511-23. doi: 10.1002/hbm.20623
Wang, L., Li, Y., Metzak, P., He, Y., & Woodward, T. S. (2010). Age-related changes in topological patterns of large-scale brain functional networks during memory encoding and recognition. Neuroimage, 50(3), 862-72. doi: 10.1016/j.neuroimage.2010.01.044
Ward, B. D., & Mazaheri, Y. (2008). Information transfer rate in fMRI experiments measured using mutual information theory. Journal of Neuroscience Methods, 167(1), 22-30. doi: 10.1016/j.jneumeth.2007.06.027
Warsi, M. A. (2012). The Fractal Nature and Functional Connectivity of Brain Function as Measured by BOLD MRI in Alzheimer’s Disease [PhD thesis]. Hamilton: McMaster University.
Xia, M., & He, Y. (2011). Magnetic resonance imaging and graph theoretical analysis of complex brain networks in neuropsychiatric disorders. Brain Connectivity, 1(5), 349-65. doi: 10.1089/brain.2011.0062
You, W., & Stadler, J. (2012). Fractal-driven distortion of resting state functional networks in fMRI: A simulation study. Paper presented at The 3rd Biennial Conference on Resting State Brain Connectivity, Magdeburg, Germany, 5-7 September 2012.
Zhang, J., Wang, J., Wu, Q., Kuang, W., Huang, X., He, Y., et al. (2011). Disrupted brain connectivity networks in drug-naive, first-episode major depressive disorder. Biological Psychiatry, 70(4), 334-342. doi: 10.1016/j.biopsych.2011.05.018
Zhang, Y., Liu, J., Li, L., Du, M., Fang, W., Wang, D., et al. (2014). A study on small-world brain functional networks altered by postherpetic neuralgia. Magnetic Resonance Imaging, 32(4), 359-365. doi: 10.1016/j.mri.2013.12.016
Zhang, Z., Liao, W., Chen, H., Mantini, D., Ding, J. R., Xu, Q., et al. (2011). Altered functional–structural coupling of large-scale brain networks in idiopathic generalized epilepsy. Brain, 134(10), 2912-28. doi: 10.1093/brain/awr223
Type of Study: Original |
Subject:
Computational Neuroscience
Received: 2016/02/28 | Accepted: 2016/05/23 | Published: 2017/09/19
Received: 2016/02/28 | Accepted: 2016/05/23 | Published: 2017/09/19
Send email to the article author
| Rights and permissions | |
 |
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License. |