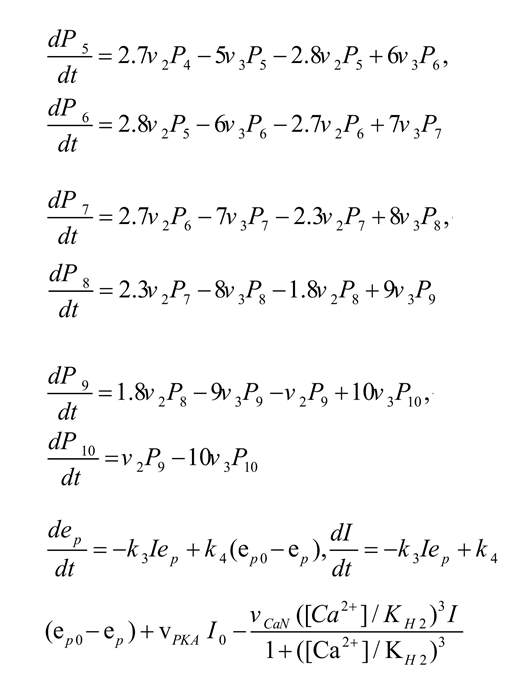Volume 9, Issue 4 (July & August 2018 2018)
BCN 2018, 9(4): 275-288 |
Back to browse issues page
Download citation:
BibTeX | RIS | EndNote | Medlars | ProCite | Reference Manager | RefWorks
Send citation to:



BibTeX | RIS | EndNote | Medlars | ProCite | Reference Manager | RefWorks
Send citation to:
Borjkhani M, Bahrami F, Janahmadi M. Assessing the Effects of Opioids on Pathological Memory by a Computational Model. BCN 2018; 9 (4) :275-288
URL: http://bcn.iums.ac.ir/article-1-962-en.html
URL: http://bcn.iums.ac.ir/article-1-962-en.html
1- Motor Control and Computational Neuroscience Laboratory, School of Electrical & Computer Engineering, College of Engineering, University of Tehran, Tehran, Iran.
2- Neuroscience Research Center, Shahid Beheshti University of Medical Sciences, Tehran, Iran.
2- Neuroscience Research Center, Shahid Beheshti University of Medical Sciences, Tehran, Iran.
Keywords: Opioids, Memory of addiction, Synaptic plasticity, Long-Term Potentiation (LTP), Hippocampus
Full-Text [PDF 3148 kb]
| Abstract (HTML)

Full-Text:
1. Introduction
Opioid consumption like other drugs can lead to behavioral changes (Contet, Kieffer, & Befort, 2004; Williams, Christie, & Manzoni, 2001). Some researchers believe that these changes are due to pathological memory formation which can be called memory of addiction (Dong & Nestler, 2014; Kelley, 2004; Nestler, 2001). Hippocampus seems to be one of the targets subject to the plastic changes due to drug abuse (Bao et al., 2007; Borjkhani, Mahdavi, & Bahrami, 2014; Capogna, Gähwiler, & Thompson, 1993; Caudle & Chavkin, 1990; Ga, 1980; Heidari et al., 2013; Hosseinmardi, Azimi, Fathollahi, Javan, & Naghdi, 2011; Hosseinmardi, Fathollahi, Naghdi, & Javan, 2009).
At the synaptic level, drug-induced changes might be due to Long-Term Potentiation (LTP)/ Long-Term Depression (LTD) induction. Therefore, analyzing LTP/LTD induction in synapses under the presence of opioids can help researchers to unveil the formation mechanisms of this pathological memory by drugs (Kauer & Malenka, 2007; Lüscher & Malenka, 2011).
Opioids affect hippocampal neurons mainly by enhancing glutamate release in presynaptic neurons (Akaishi, Saito, Ito, Ishige, & Ikegaya, 2000; Williams et al., 2001) and increasing postsynaptic receptors activities (Kauer & Malenka, 2007; van Huijstee & Mansvelder, 2015; Williams et al., 2001). All the modifications caused by opioids result in LTP induction in affected synapses (Bao et al., 2007; Wolf, 2003). It has been shown that one of the causes of LTP induction is Calmodulin-dependent protein Kinase II (CaMKII) phosphorylation process (Lisman, Yasuda, & Raghavachari, 2012; Sanhueza & Lisman, 2013).
On the other hand, Ca2+ concentration is the main mediator in this process. Elevation of Ca2+ concentration in postsynaptic neuron triggers CaMKII phosphorylation process. Ca2+ can enter into the neuron through Voltage-Gated Calcium Channels (VGCCs), N-Methyl-D-Aspartate Receptor (NMDAR) and Ca2+ permeable α-Amino-3-hydroxy-5-methyl-4-isoxazole Propionic Acid Receptors (AMPARs). Thus, these channels and receptors contribute in CaMKII phosphorylation process and LTP induction.
It has been shown that blocking hippocampal VGCCs can prevent opioids dependency (Mishra, Barik, & Ray, 2017). Furthermore, opioid effects on NMDARs and AMPARs were verified in different research studies (Capogna et al., 1993; Chen & Huang, 1992; Chen & Marine, 1991; Ga, 1980; Kauer & Malenka, 2007; Nestler, 2013; Peters & De Vries, 2012; Williams et al., 2001). Most of the research and findings in this field are based on experimental observations.
However, computational models offer new tools and approaches for investigating neurophysiological basis of addiction memory formation process. In general, computational modeling of biological systems helps us to study consistency of different experimental findings and to predict the behavior of a given biological system under different constraints. That is why computational modeling has recently attracted the interests of many researchers in the field of neuroscience (Amiri, Bahrami, & Janahmadi, 2012; Amiri, Montaseri, & Bahrami, 2011; Li et al., 2016; Tewari & Majumdar, 2012b; Volman, Bazhenov, & Sejnowski, 2012).
Therefore, in this paper, using experimental findings we introduce a minimal computational model to assess opioid-induced LTP in CA1 region of the hippocampus. This model can also be used for analyzing the effects of other drugs by minor modifications. In the first part of the paper, opioids effect on hippocampal neurons will be discussed. The second part is dedicated to introduce mathematical modeling approach. The third part presents simulation results. Discussion and conclusion will be presented in the final part.
2. Methods
2.1 Neurophysiological background
According to many research studies, opioid-induced modifications in glutamatergic synapses are responsible for pathological memory formation related to the addiction (Harris, Wimmer, Byrne, & Aston-Jones, 2004; Herman et al., 2003; Mameli, Bellone, Brown, & Lüscher, 2011; van Huijstee & Mansvelder, 2015). Since Long-Term Potentiation (LTP)/ Long-Term Depression (LTD) induction can be considered as signs of memory formation process at the synaptic level, one can also suggest that addiction memory formation might occur through the induction of LTP/LTD.
It has been shown that opioids induce LTP in hippocampal synapses by two primary mechanisms: 1. Enhancing glutamate release through disinhibitory mechanism (Capogna et al., 1993; Caudle & Chavkin, 1990; Cohen, Doze, & Madison, 1992; Rezai, Kieffer, Roux, & Massotte, 2013); and 2. By manipulating postsynaptic NMDARs current (Chen & Huang, 1992; Chen & Marine, 1991; Kow, Commons, Ogawa, & Pfaff, 2002; van Huijstee & Mansvelder, 2015). Opioids modify NMDARs current by increasing conduction of NMDARs and inhibiting Mg2+ from blocking NMDA receptors (Chen & Huang, 1992; Chen & Marine, 1991; Herman et al., 2003).
Consequently, these changes in synaptic transmission result in more calcium flux into the postsynaptic neuron (Kow et al., 2002; Przewlocki et al., 1999). Enhancement of postsynaptic calcium can activate CAMKII mechanisms (Herman et al., 2003; Trujillo, 2002). Phosphorylation of CaMKII leads to LTP induction and can be seen as molecular memory formation (Kauer & Malenka, 2007; Lisman et al., 2012; Sanhueza & Lisman, 2013). Furthermore, enhancement of postsynaptic calcium can lead to phosphorylation of AMPARs (Castellani, Quinlan, Bersani, Cooper, & Shouval, 2005; Castellani, Quinlan, Cooper, & Shouval, 2001; Kauer & Malenka, 2007).
Also, it has been shown that VGCCs are involved in opioids dependency (Bongianni, Carla, Moroni, & Pellegrini‐Giampietro, 1986; Mishra et al., 2017). To investigate the mechanism of a false LTP induced by opioids, we developed a computational model of a postsynaptic neuron in CA1 region. In this model, we considered all important aspects mentioned from these neurophysiological studies. This model will be described in the next part (Figure 1).
2.2. Computational modeling approach
To analysis opioid-induced synaptic plasticity in CA1 region of the hippocampus, the spine of a CA1 pyramidal neuron is modeled by Equation (1):
Opioid consumption like other drugs can lead to behavioral changes (Contet, Kieffer, & Befort, 2004; Williams, Christie, & Manzoni, 2001). Some researchers believe that these changes are due to pathological memory formation which can be called memory of addiction (Dong & Nestler, 2014; Kelley, 2004; Nestler, 2001). Hippocampus seems to be one of the targets subject to the plastic changes due to drug abuse (Bao et al., 2007; Borjkhani, Mahdavi, & Bahrami, 2014; Capogna, Gähwiler, & Thompson, 1993; Caudle & Chavkin, 1990; Ga, 1980; Heidari et al., 2013; Hosseinmardi, Azimi, Fathollahi, Javan, & Naghdi, 2011; Hosseinmardi, Fathollahi, Naghdi, & Javan, 2009).
At the synaptic level, drug-induced changes might be due to Long-Term Potentiation (LTP)/ Long-Term Depression (LTD) induction. Therefore, analyzing LTP/LTD induction in synapses under the presence of opioids can help researchers to unveil the formation mechanisms of this pathological memory by drugs (Kauer & Malenka, 2007; Lüscher & Malenka, 2011).
Opioids affect hippocampal neurons mainly by enhancing glutamate release in presynaptic neurons (Akaishi, Saito, Ito, Ishige, & Ikegaya, 2000; Williams et al., 2001) and increasing postsynaptic receptors activities (Kauer & Malenka, 2007; van Huijstee & Mansvelder, 2015; Williams et al., 2001). All the modifications caused by opioids result in LTP induction in affected synapses (Bao et al., 2007; Wolf, 2003). It has been shown that one of the causes of LTP induction is Calmodulin-dependent protein Kinase II (CaMKII) phosphorylation process (Lisman, Yasuda, & Raghavachari, 2012; Sanhueza & Lisman, 2013).
On the other hand, Ca2+ concentration is the main mediator in this process. Elevation of Ca2+ concentration in postsynaptic neuron triggers CaMKII phosphorylation process. Ca2+ can enter into the neuron through Voltage-Gated Calcium Channels (VGCCs), N-Methyl-D-Aspartate Receptor (NMDAR) and Ca2+ permeable α-Amino-3-hydroxy-5-methyl-4-isoxazole Propionic Acid Receptors (AMPARs). Thus, these channels and receptors contribute in CaMKII phosphorylation process and LTP induction.
It has been shown that blocking hippocampal VGCCs can prevent opioids dependency (Mishra, Barik, & Ray, 2017). Furthermore, opioid effects on NMDARs and AMPARs were verified in different research studies (Capogna et al., 1993; Chen & Huang, 1992; Chen & Marine, 1991; Ga, 1980; Kauer & Malenka, 2007; Nestler, 2013; Peters & De Vries, 2012; Williams et al., 2001). Most of the research and findings in this field are based on experimental observations.
However, computational models offer new tools and approaches for investigating neurophysiological basis of addiction memory formation process. In general, computational modeling of biological systems helps us to study consistency of different experimental findings and to predict the behavior of a given biological system under different constraints. That is why computational modeling has recently attracted the interests of many researchers in the field of neuroscience (Amiri, Bahrami, & Janahmadi, 2012; Amiri, Montaseri, & Bahrami, 2011; Li et al., 2016; Tewari & Majumdar, 2012b; Volman, Bazhenov, & Sejnowski, 2012).
Therefore, in this paper, using experimental findings we introduce a minimal computational model to assess opioid-induced LTP in CA1 region of the hippocampus. This model can also be used for analyzing the effects of other drugs by minor modifications. In the first part of the paper, opioids effect on hippocampal neurons will be discussed. The second part is dedicated to introduce mathematical modeling approach. The third part presents simulation results. Discussion and conclusion will be presented in the final part.
2. Methods
2.1 Neurophysiological background
According to many research studies, opioid-induced modifications in glutamatergic synapses are responsible for pathological memory formation related to the addiction (Harris, Wimmer, Byrne, & Aston-Jones, 2004; Herman et al., 2003; Mameli, Bellone, Brown, & Lüscher, 2011; van Huijstee & Mansvelder, 2015). Since Long-Term Potentiation (LTP)/ Long-Term Depression (LTD) induction can be considered as signs of memory formation process at the synaptic level, one can also suggest that addiction memory formation might occur through the induction of LTP/LTD.
It has been shown that opioids induce LTP in hippocampal synapses by two primary mechanisms: 1. Enhancing glutamate release through disinhibitory mechanism (Capogna et al., 1993; Caudle & Chavkin, 1990; Cohen, Doze, & Madison, 1992; Rezai, Kieffer, Roux, & Massotte, 2013); and 2. By manipulating postsynaptic NMDARs current (Chen & Huang, 1992; Chen & Marine, 1991; Kow, Commons, Ogawa, & Pfaff, 2002; van Huijstee & Mansvelder, 2015). Opioids modify NMDARs current by increasing conduction of NMDARs and inhibiting Mg2+ from blocking NMDA receptors (Chen & Huang, 1992; Chen & Marine, 1991; Herman et al., 2003).
Consequently, these changes in synaptic transmission result in more calcium flux into the postsynaptic neuron (Kow et al., 2002; Przewlocki et al., 1999). Enhancement of postsynaptic calcium can activate CAMKII mechanisms (Herman et al., 2003; Trujillo, 2002). Phosphorylation of CaMKII leads to LTP induction and can be seen as molecular memory formation (Kauer & Malenka, 2007; Lisman et al., 2012; Sanhueza & Lisman, 2013). Furthermore, enhancement of postsynaptic calcium can lead to phosphorylation of AMPARs (Castellani, Quinlan, Bersani, Cooper, & Shouval, 2005; Castellani, Quinlan, Cooper, & Shouval, 2001; Kauer & Malenka, 2007).
Also, it has been shown that VGCCs are involved in opioids dependency (Bongianni, Carla, Moroni, & Pellegrini‐Giampietro, 1986; Mishra et al., 2017). To investigate the mechanism of a false LTP induced by opioids, we developed a computational model of a postsynaptic neuron in CA1 region. In this model, we considered all important aspects mentioned from these neurophysiological studies. This model will be described in the next part (Figure 1).
2.2. Computational modeling approach
To analysis opioid-induced synaptic plasticity in CA1 region of the hippocampus, the spine of a CA1 pyramidal neuron is modeled by Equation (1):
This Equation denotes a minimal model to produce Excitatory Postsynaptic Potentials (EPSPs) based on Tsodyks and Markram’s passive membrane model (Tsodyks & Markram, 1997), where τpost shows time constant of neuron membrane, Vrestpost denotes neuron’s membrane potential at rest, and Rm denotes actual resistance of spin. The synaptic current denoted by Isyn can be described by:
Here, IAMPA and INMDA are AMPAR and NMDAR currents, respectively. Model of AMPAR current is based on Destexhe’s model (Destexhe, Mainen, & Sejnowski, 1998):
Where VAMPA refers to reversal potential of the receptor, Vpost is the membrane potential, and mAMPA denotes gating variable of AMPAR. Gating variable of AMPAR can be represented by the following Equation (Destexhe, Mainen, & Sejnowski, 1998):
Here opening and closing rate of the receptor are shown by αampa and βampa, respectively, gpre shows glutamate concentration, gAMPA described in Equation (3) denotes AMPAR’s channel conductance that can be enhanced due to CaMKII phosphorylation process by using the following Equation:
Where gAMPA0=0.4 nS is the initial value for AMPAR’s conductance, Phalf=40 µM and khalf=0.4 µM are constants which enables AMPAR conductance to increase through CaMKII phosphorylation process. Model of the NMDAR current can described by the following Equation (Destexhe, Mainen, & Sejnowski, 1998; Moradi et al., 2013):
Where VNMDA shows the reversal potential of NMDAR, opening and closing rate of receptor are shown by αNMDAand βNMDA respectively, Op refers to opioids concentration in the synapse, and gpre shows glutamate concentration. NMDA channels conductance (gNMDA) is represented by the following Equation:
, where gVI and gVD are voltage-independent and voltage-dependent conductance. The latter conductance is described by:
Here, gVD,∞ is the final value of gVD, τg denotes time constant, gVD,∞ , and Vpost has a linear relation with constant of K. Other parameters and their values have been listed in the Appendix.
Calcium can enter into the neuron through AMPARs, NMDARs, and VGCCs. Also, calcium pumps are responsible for transferring the calcium out of the neuron. So, calcium concentration inside the neuron can be represented by the following Equation (Tewari & Majumdar, 2012b:
Calcium can enter into the neuron through AMPARs, NMDARs, and VGCCs. Also, calcium pumps are responsible for transferring the calcium out of the neuron. So, calcium concentration inside the neuron can be represented by the following Equation (Tewari & Majumdar, 2012b:
Here, Cpost shows postsynaptic calcium concentration, IR denotes voltage-gated calcium channels activation, and Spump refers to pumped calcium. Here, η=0.012 and y=0.06 demonstrate the amount of calcium that can enter into the neuron through AMPARs and NMDARs. Zca=2 denotes calcium valence, F=96487C/mo l is the faraday’s constant, and Vspine=0.9048 µM3 is the volume for dendrite spin. Furthermore, bt=200 µM shows total endogenous buffer concentration and Kendo=10 µM denotes endogenous buffer calcium affinity. Pumped calcium is represented by the following Equation (Tewari & Majumdar, 2012b):
Here, Ks=100/s is the maximum efflux rate of calcium pump, Crestpost=100nM is the rest value for postsynaptic calcium concentration, and VGCCs activation is represented by the following Equation (Tewari & Majumdar, 2012b):
, where gR=15ps is the conductance of calcium channel, B(N, Popen) denotes a random variable with a binomial distribution which shows the number of opened channels, and VR=27.4mv denotes the reversal potential.
Phosphorylation of CaMKII due to calcium concentration can be described by the following Equation (Zhabotinsky, 2000):
Phosphorylation of CaMKII due to calcium concentration can be described by the following Equation (Zhabotinsky, 2000):
, where Pi shows the concentration of the i-fold phosphorylated CaMKII, ep refers to the PP1 concentration which is not bounded to l1P and may demonstrate active protein phosphatase, the total concentration of PP1 is shown by ep0=0.1 µM, free l1P is denoted by I, and free l1 concentration is shown by I0=0.1 µM. Also K3=1/ µMs and K3=10-3/s are association and dissociation rate constant of PP1-l1P complex, respectively. vcaN=2/s refers to the rate of l1P dephosphorylation due to calcineurin (CaN), VPKA=0.45 µM/sis the phosphorylation rate of l1 due to the protein kinase A (PKA), and KH2=0.7 µM is the calcium activation Hill constant of CaN.
Phosphorylation (V1), auto-phosphorylation (V2), and dephosphorylation (V3) rates can be represented by the following equations:
Phosphorylation (V1), auto-phosphorylation (V2), and dephosphorylation (V3) rates can be represented by the following equations:
, where k1=0.5/s is the l1 dependent regulation rate of PP1 and KH1=4 µM is the Hill constant of CaMKII for calcium activation. KM=20 µM and are K2=10/s the Michaelis and catalytic constants, respectively. Finally, phosphorylated CaMKII can be presented by:
In the next part, simulation results are presented.
3. Results
The mathematical modeling approach simulation results are presented in this section. Simulations were implemented in Matlab 2014a. To solve differential equations, the forward Euler method with constant step size of 0.05 ms is used. Synaptic glutamate is assumed as a periodic signal with a frequency of 5 Hz which each pulse has a duration of 4 ms. The amplitude of this signal is 0.2 mM and the simulation time is 10 s. In all Figures, 1 second of the simulation is depicted to clarify dynamics of the signals.
3.1. Normal and pathological conditions
One of the features of opioid-induced synaptic plasticity is the induction of LTP where normal LTP cannot occur (van Huijstee & Mansvelder, 2015). Therefore, stimulation signal (which is synaptic glutamate) is considered as a pulse train with a frequency of 5 Hz and amplitude of 0.2 mM. Choosing these values are based on experimental observations used by Tewari and Majumdar’s computational models (Tewari & Majumdar, 2012b; Tewari & Majumdar, 2012a).
3. Results
The mathematical modeling approach simulation results are presented in this section. Simulations were implemented in Matlab 2014a. To solve differential equations, the forward Euler method with constant step size of 0.05 ms is used. Synaptic glutamate is assumed as a periodic signal with a frequency of 5 Hz which each pulse has a duration of 4 ms. The amplitude of this signal is 0.2 mM and the simulation time is 10 s. In all Figures, 1 second of the simulation is depicted to clarify dynamics of the signals.
3.1. Normal and pathological conditions
One of the features of opioid-induced synaptic plasticity is the induction of LTP where normal LTP cannot occur (van Huijstee & Mansvelder, 2015). Therefore, stimulation signal (which is synaptic glutamate) is considered as a pulse train with a frequency of 5 Hz and amplitude of 0.2 mM. Choosing these values are based on experimental observations used by Tewari and Majumdar’s computational models (Tewari & Majumdar, 2012b; Tewari & Majumdar, 2012a).
As it is shown, synaptic glutamate activates AMPARs and NMDARs. By activation of these receptors, calcium enters into the neuron through VGCCs, NMDARs, and AMPARs. Activation of calcium pumps decreases calcium concentration in the neuron. Elevation of calcium may lead to activation of CaMKII mechanism which enhances AMPAR conductance.
The plain black bar is the phosphorylated CaMKII, and the green bar with black patterns is the phosphorylated AMPAR. Horizontal axes with “normal” label shows simulation in normal condition, “Opioid” label shows opioid injected condition, “CK=0” stands for the simulation in which opioid effect on NMDAR's conductance is assumed as 0, “CMg=0” describes the state that opioid effect on Mg2+ blocking is assumed as 0 and “Icr=0” refers to the case that current mediated by VGCC is assumed as 0.
Applying synaptic glutamate (Figure 2a) leads to AMPARs activation (Figure 2b) which depolarize membrane potential. Depolarized membrane allows NMDARs activation by removing Mg2+ blocking (Figure 2c). Since high-voltage calcium channels are considered in the model, calcium channels activation is 0 which is described in Figure 2d. Ions of Ca2+ can enter into the neuron through AMPARs and NMDARs activation. So, Ca2 concentration enhances in the neuron which is shown in Figure 2e. Entered Ca2+ can engage in CaMKII phosphorylation process, however, due to lack of enough calcium, this process is not observed here (Figure 2f). Based on simulation results, none of the AMPARs can phosphorylate (Figure 2g). Generally, this simulation can describe the normal condition which there is not any opioid’s effect in the synapse. In this simulation, LTP does not occur in the synapse due to lack of phosphorylated CaMKII and AMPARs.
Applying 1 μM of opioid increases NMDARs activation through inhibition of Mg2+ blocking and enhancement of receptors conductance. NMDAR mediated current enhances in this situation (Figure 3c). Thus, more calcium enters into the neuron (Figure 3e) which triggers CaMKII phosphorylation process (Figure 3f). Furthermore, more activation of NMDARs results in VGCCs activation. Figure 3d shows calcium current mediated by VGCCs. Exceeding phosphorylated CaMKII from a predetermined threshold can phosphorylate AMPARs. In fact, AMPAR conductance increases which is shown in Figure 3g. Thus more current is mediated by AMPARs (Figure 3b) that can work as a positive feedback for enhancement of calcium concentration in the neuron.
3.2. Comparing different factors on pathological LTP induction
Simulation results show that injection of opioid can induce LTP when normal LTP does not occur. Now we want to assess which components of the model are responsible in inducing such a pathological LTP. Based on these simulations we can suggest a way to prevent this type of pathological LTP.
Applying synaptic glutamate (Figure 2a) leads to AMPARs activation (Figure 2b) which depolarize membrane potential. Depolarized membrane allows NMDARs activation by removing Mg2+ blocking (Figure 2c). Since high-voltage calcium channels are considered in the model, calcium channels activation is 0 which is described in Figure 2d. Ions of Ca2+ can enter into the neuron through AMPARs and NMDARs activation. So, Ca2 concentration enhances in the neuron which is shown in Figure 2e. Entered Ca2+ can engage in CaMKII phosphorylation process, however, due to lack of enough calcium, this process is not observed here (Figure 2f). Based on simulation results, none of the AMPARs can phosphorylate (Figure 2g). Generally, this simulation can describe the normal condition which there is not any opioid’s effect in the synapse. In this simulation, LTP does not occur in the synapse due to lack of phosphorylated CaMKII and AMPARs.
Applying 1 μM of opioid increases NMDARs activation through inhibition of Mg2+ blocking and enhancement of receptors conductance. NMDAR mediated current enhances in this situation (Figure 3c). Thus, more calcium enters into the neuron (Figure 3e) which triggers CaMKII phosphorylation process (Figure 3f). Furthermore, more activation of NMDARs results in VGCCs activation. Figure 3d shows calcium current mediated by VGCCs. Exceeding phosphorylated CaMKII from a predetermined threshold can phosphorylate AMPARs. In fact, AMPAR conductance increases which is shown in Figure 3g. Thus more current is mediated by AMPARs (Figure 3b) that can work as a positive feedback for enhancement of calcium concentration in the neuron.
3.2. Comparing different factors on pathological LTP induction
Simulation results show that injection of opioid can induce LTP when normal LTP does not occur. Now we want to assess which components of the model are responsible in inducing such a pathological LTP. Based on these simulations we can suggest a way to prevent this type of pathological LTP.
Further simulations were performed to analyze different parameters involved in inducing pathological LTP. Normalized value for phosphorylated CaMKII and AMPARs are calculated in each simulation. The values are calculated by using the following Equation:
Where YNormalized refers to the normalized value, Y is the parameter value, also YMax and YMin denote maximum and minimum values of the parameter, respectively. This normalization approach results in normalized values within [0-1] interval.
Opioid-induced LTP were analyzed with 3 different assumptions: 1. Opioid does not modify NMDARs conductance; 2. Opioid does not have any infulence on Mg2+ blocking; and 3. VGCCs mediated current is 0. Simulation results according to the assumptions are shown in Figure 4. In normal condition, phosphorylated CaMKII and AMPAR is 0 which specifies there is not any step foot of LTP in the synapse. Presence of opioid leads to phosphorylation of CaMKII and AMPAR, and normalized values are in the high state. This simulation demonstrates the presence of LTP in the synapse.
It can be seen that LTP does not occur in the synapse by neglecting opioid effect on NMDAR’s conductance (CK=0 label in Figure 4). Although, neglecting opioid’s effect on Mg2+ blocking (CMg=0 label in Figure 4) is not a critical parameter, knocking out VGCC’s activation leads to attenuation of the LTP (Icr=0 label in Figure 4). These results show that enhancement of NMDAR’s conductance besides VGCC’s activation is a fundamental parameter in inducing pathological LTP. Therefore in the next part, constants for VGCC’s activation and NMDAR’s conductance are changed for further simulations.
The left panel of Figure 5 shows the normalized value for phosphorylated CaMKII and AMPAR with a variable coefficient of NMDAR’s conductance. It can be seen that when the coefficient is 0.2, there is not any phosphorylation; however, when it is 0.3, CaMKII and AMPAR phosphorylate. It means that attenuation of LTP by manipulating NMDAR’s conductance is impossible. We can whether completely block LTP or not, and there is nothing in between. However, according to the simulation results shown in right panel of Figure 5, increment in VGCC mediated current strengthens LTP. As a matter of fact, increasing channels activation constant intensifies LTP.
Besides opioid’s direct effect on postsynaptic neurons, change in frequency and amplitude of stimulation signal which are considered as synaptic glutamate can alter pathological LTP. The left panel of Figure 6 shows the variation of glutamate on the CaMKII and AMPAR phosphorylation process. This simulation shows that reducing glutamate amplitude by 0.01 increments from 0.2 does not lead to inhibition of LTP until glutamate amplitude reaches 0.14. At this value, phosphorylated CaMKII and AMPARs decline rapidly, and LTP does not occur. However, a gradual decrease in stimulation frequency leads to gradual descend in LTP induction shown in the right panel of Figure 6.
4. Discussion
Our simulation results support the hypothesis that opioids consumption can lead to pathological memory formation in hippocampal neurons through induction of LTP. To explain this issue, we developed a computational model in which CaMKII and AMPAR phosphorylation processes are considered as foot prints of LTP induction.
Experimental observations (Chen & Huang, 1992; Chen & Marine, 1991; Kow et al., 2002; Mao, 1999) indicate the opioids effects on NMDARs. Enhancement of NMDAR mediated current is a byproduct of opioids presence in synapses. Our simulation results showed that enhancement of NMDAR’s conductance is more efficient in inducing LTP compared to inhibition of Mg2+ blocking through opioids. In other words, despite the inhibitory effect of Mg2+ blocking on NMDAR mediated current, we observed that the main reason of LTP induction is enhancement of NMDA receptors conductance. Furthermore, our results suggest that prevention of pathological LTP can be achieved by blocking NMDAR’s conductance. NMDAR’s conductance acts like a none-or-all switch in inducing LTP. Therefore, it is impossible to attenuate pathological LTP by decreasing NMDAR’s conductance. However, we may completely block it using this approach.
Bongianni et al. (1986) and Mishra et al. (2017), through their experimental observations, suggested that blocking VGCCs leads to preventing dependency on opioids. In this research, we obtained the same result but in a different way, i.e., we showed the role of VGCCs in forming pathological LTP. Our simulation results demonstrate that by inhibiting VGCCs, pathological LTP is attenuated. Also, we may infer that by decreasing VGCC activation, pathological LTP is gradually lessened. One may be able to apply this finding in cases where one intends or prefers to attenuate pathological LTP rather than blocking it.
On the other hand, disinhibitory effect of opioid increases glutamate concentration in the synaptic cleft. Therefore, it is reasonable to assume that changes in the amplitude and the frequency of the stimulation signal in the postsynaptic neuron are due to the presence of the opioid. Simulation results demonstrate that increasing the frequency and the amplitude of the stimulation signal results in LTP induction. There are different experimental observations that support these simulation results (Akaishi et al., 2000; Capogna et al., 1993; Caudle & Chavkin, 1990; Cohen et al., 1992; Kauer & Malenka, 2007; Rezai et al., 2013).
These observations indicate that opioid inhibits the GABAergic signal that leads to enhancement of glutamate concentration in the synapse. Furthermore, our simulation results suggest that reducing synaptic glutamate can prevent pathological LTP induction. Amplitude and frequency of glutamate release are parameters that will help in preventing or attenuating LTP. Since the source of glutamate is mainly from presynaptic neurons, inhibition of presynaptic pyramidal neurons may help prevent pathological LTP induction. On the other hand, one of the fundamental functions of the glial cells is reuptake of the synaptic glutamate. Therefore, we also suggest considering the role of glial cells in preventing pathological memory formation. This goal can be achieved through stimulating glutamate transporters. Using this approach, synaptic glutamate can be reduced, and this can result in reducing stimulation of the postsynaptic receptors.
In this paper, we introduced a computational model for postsynaptic neurons in CA1 region of the hippocampus to examine LTP induction due to opioids. The model is consisted of a spine which produces EPSPs. NMDAR, AMPAR and VGCC’s mediated currents are also considered in the model. Calcium ions flow into the neuron through these channels and receptors. Elevation of calcium concentration leads to CaMKII and AMPAR phosphorylation. We assumed that CaMKII and AMPAR phosphorylation are foot prints of LTP induction.
Simulation results of the presented model indicate that presence of opioids can lead to LTP induction in a situation that normal LTP does not occur. This finding supports the idea that opioids may form a memory that is directly linked to drug consumption. Therefore, one of the primary triggers of relapse in withdrawal time is this pathological memory. Furthermore, we observed that, by decreasing VGCC’s activation, NMDAR’s activation, and glutamate concentration in the synapse, pathological LTP reduces and it is even possible to prevent the pathological LTP.
Ethical Considerations
Compliance with ethical guidelines
Since the research was a simulation one, the authors did not need to get any ethical approvals.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Conflict of interest
The authors declared no conflict of interest.
References
Opioid-induced LTP were analyzed with 3 different assumptions: 1. Opioid does not modify NMDARs conductance; 2. Opioid does not have any infulence on Mg2+ blocking; and 3. VGCCs mediated current is 0. Simulation results according to the assumptions are shown in Figure 4. In normal condition, phosphorylated CaMKII and AMPAR is 0 which specifies there is not any step foot of LTP in the synapse. Presence of opioid leads to phosphorylation of CaMKII and AMPAR, and normalized values are in the high state. This simulation demonstrates the presence of LTP in the synapse.
It can be seen that LTP does not occur in the synapse by neglecting opioid effect on NMDAR’s conductance (CK=0 label in Figure 4). Although, neglecting opioid’s effect on Mg2+ blocking (CMg=0 label in Figure 4) is not a critical parameter, knocking out VGCC’s activation leads to attenuation of the LTP (Icr=0 label in Figure 4). These results show that enhancement of NMDAR’s conductance besides VGCC’s activation is a fundamental parameter in inducing pathological LTP. Therefore in the next part, constants for VGCC’s activation and NMDAR’s conductance are changed for further simulations.
The left panel of Figure 5 shows the normalized value for phosphorylated CaMKII and AMPAR with a variable coefficient of NMDAR’s conductance. It can be seen that when the coefficient is 0.2, there is not any phosphorylation; however, when it is 0.3, CaMKII and AMPAR phosphorylate. It means that attenuation of LTP by manipulating NMDAR’s conductance is impossible. We can whether completely block LTP or not, and there is nothing in between. However, according to the simulation results shown in right panel of Figure 5, increment in VGCC mediated current strengthens LTP. As a matter of fact, increasing channels activation constant intensifies LTP.
Besides opioid’s direct effect on postsynaptic neurons, change in frequency and amplitude of stimulation signal which are considered as synaptic glutamate can alter pathological LTP. The left panel of Figure 6 shows the variation of glutamate on the CaMKII and AMPAR phosphorylation process. This simulation shows that reducing glutamate amplitude by 0.01 increments from 0.2 does not lead to inhibition of LTP until glutamate amplitude reaches 0.14. At this value, phosphorylated CaMKII and AMPARs decline rapidly, and LTP does not occur. However, a gradual decrease in stimulation frequency leads to gradual descend in LTP induction shown in the right panel of Figure 6.
4. Discussion
Our simulation results support the hypothesis that opioids consumption can lead to pathological memory formation in hippocampal neurons through induction of LTP. To explain this issue, we developed a computational model in which CaMKII and AMPAR phosphorylation processes are considered as foot prints of LTP induction.
Experimental observations (Chen & Huang, 1992; Chen & Marine, 1991; Kow et al., 2002; Mao, 1999) indicate the opioids effects on NMDARs. Enhancement of NMDAR mediated current is a byproduct of opioids presence in synapses. Our simulation results showed that enhancement of NMDAR’s conductance is more efficient in inducing LTP compared to inhibition of Mg2+ blocking through opioids. In other words, despite the inhibitory effect of Mg2+ blocking on NMDAR mediated current, we observed that the main reason of LTP induction is enhancement of NMDA receptors conductance. Furthermore, our results suggest that prevention of pathological LTP can be achieved by blocking NMDAR’s conductance. NMDAR’s conductance acts like a none-or-all switch in inducing LTP. Therefore, it is impossible to attenuate pathological LTP by decreasing NMDAR’s conductance. However, we may completely block it using this approach.
Bongianni et al. (1986) and Mishra et al. (2017), through their experimental observations, suggested that blocking VGCCs leads to preventing dependency on opioids. In this research, we obtained the same result but in a different way, i.e., we showed the role of VGCCs in forming pathological LTP. Our simulation results demonstrate that by inhibiting VGCCs, pathological LTP is attenuated. Also, we may infer that by decreasing VGCC activation, pathological LTP is gradually lessened. One may be able to apply this finding in cases where one intends or prefers to attenuate pathological LTP rather than blocking it.
On the other hand, disinhibitory effect of opioid increases glutamate concentration in the synaptic cleft. Therefore, it is reasonable to assume that changes in the amplitude and the frequency of the stimulation signal in the postsynaptic neuron are due to the presence of the opioid. Simulation results demonstrate that increasing the frequency and the amplitude of the stimulation signal results in LTP induction. There are different experimental observations that support these simulation results (Akaishi et al., 2000; Capogna et al., 1993; Caudle & Chavkin, 1990; Cohen et al., 1992; Kauer & Malenka, 2007; Rezai et al., 2013).
These observations indicate that opioid inhibits the GABAergic signal that leads to enhancement of glutamate concentration in the synapse. Furthermore, our simulation results suggest that reducing synaptic glutamate can prevent pathological LTP induction. Amplitude and frequency of glutamate release are parameters that will help in preventing or attenuating LTP. Since the source of glutamate is mainly from presynaptic neurons, inhibition of presynaptic pyramidal neurons may help prevent pathological LTP induction. On the other hand, one of the fundamental functions of the glial cells is reuptake of the synaptic glutamate. Therefore, we also suggest considering the role of glial cells in preventing pathological memory formation. This goal can be achieved through stimulating glutamate transporters. Using this approach, synaptic glutamate can be reduced, and this can result in reducing stimulation of the postsynaptic receptors.
In this paper, we introduced a computational model for postsynaptic neurons in CA1 region of the hippocampus to examine LTP induction due to opioids. The model is consisted of a spine which produces EPSPs. NMDAR, AMPAR and VGCC’s mediated currents are also considered in the model. Calcium ions flow into the neuron through these channels and receptors. Elevation of calcium concentration leads to CaMKII and AMPAR phosphorylation. We assumed that CaMKII and AMPAR phosphorylation are foot prints of LTP induction.
Simulation results of the presented model indicate that presence of opioids can lead to LTP induction in a situation that normal LTP does not occur. This finding supports the idea that opioids may form a memory that is directly linked to drug consumption. Therefore, one of the primary triggers of relapse in withdrawal time is this pathological memory. Furthermore, we observed that, by decreasing VGCC’s activation, NMDAR’s activation, and glutamate concentration in the synapse, pathological LTP reduces and it is even possible to prevent the pathological LTP.
Ethical Considerations
Compliance with ethical guidelines
Since the research was a simulation one, the authors did not need to get any ethical approvals.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Conflict of interest
The authors declared no conflict of interest.
References
- Akaishi, T., Saito, H., Ito, Y., Ishige, K., & Ikegaya, Y. (2000). Morphine augments excitatory synaptic transmission in the dentate gyrus through GABAergic disinhibition. Neuroscience Research, 38(4), 357-63. [DOI:10.1016/S0168-0102(00)00177-2]
- Amiri, M., Bahrami, F., & Janahmadi, M. (2012). On the role of astrocytes in epilepsy: A functional modeling approach. Neuroscience Research, 72(2), 172-80. [DOI:10.1016/j.neures.2011.11.006] [PMID]
- Amiri, M., Montaseri, G., & Bahrami, F. (2011). On the role of astrocytes in synchronization of two coupled neurons: A mathematical perspective. Biological Cybernetics, 105(2), 153-66. [DOI:10.1007/s00422-011-0455-5] [PMID]
- Bao, G., Kang, L., Li, H., Li, Y., Pu, L., Xia, P., et al. (2007). Morphine and heroin differentially modulate in vivo hippocampal LTP in opiate-dependent rat. Neuropsychopharmacology, 32(8), 1738-49. [DOI:10.1038/sj.npp.1301308] [PMID]
- Bongianni, F., Carla, V., Moroni, F., & Pellegrini‐Giampietro, D. (1986). Calcium channel inhibitors suppress the morphine‐withdrawal syndrome in rats. British Journal of Pharmacology, 88(3), 561-7. [DOI:10.1111/j.1476-5381.1986.tb10236.x] [PMID] [PMCID]
- Borjkhani, M., Mahdavi, A., & Bahrami, F. (2014). A mathematical model for neuron astrocytes interactions in hippocampus during addiction. Paper presented at the Iranian Conference on Biomedical Engineering (ICBME), Tehran, Iran, 26-28 November 2014. [DOI:10.1109/ICBME.2014.7043940]
- Capogna, M., Gähwiler, B. H., & Thompson, S. M. (1993). Mechanism of mu-opioid receptor-mediated presynaptic inhibition in the rat hippocampus in vitro. The Journal of Physiology, 470(1), 539-58.[DOI:10.1113/jphysiol.1993.sp019874]
- Castellani, G. C., Quinlan, E. M., Bersani, F., Cooper, L. N., & Shouval, H. Z. (2005). A model of bidirectional synaptic plasticity: From signaling network to channel conductance. Learning & Memory, 12(4), 423-32. [DOI:10.1101/lm.80705] [PMID] [PMCID]
- Castellani, G. C., Quinlan, E. M., Cooper, L. N., & Shouval, H. Z. (2001). A biophysical model of bidirectional synaptic plasticity: dependence on AMPA and NMDA receptors. Proceedings of the National Academy of Sciences, 98(22), 12772-7. [DOI:10.1073/pnas.201404598] [PMID] [PMCID]
- Caudle, R., & Chavkin, C. (1990). Mu opioid receptor activation reduces inhibitory postsynaptic potentials in hippocampal CA3 pyramidal cells of rat and guinea pig. Journal of Pharmacology and Experimental Therapeutics, 252(3), 1361-9. [PMID]
- Chen, L., & Huang, L. Y. M. (1992). Protein kinase C reduces Mg2+ block of NMDA-receptor channels as a mechanism of modulation. Nature, 356(6369), 521-3. [DOI:10.1038/356521a0]
- Chen, L., & Marine, L. Y. M. H. (1991). Sustained potentiation of NMDA receptor-mediated glutamate responses through activation of protein kinase C by a μ opioid. Neuron, 7(2), 319-26. [DOI:10.1016/0896-6273(91)90270-A]
- Cohen, G. A., Doze, V. A., & Madison, D. V. (1992). Opioid inhibition of GABA release from presynaptic terminals of rat hippocampal interneurons. Neuron, 9(2), 325-35. [DOI:10.1016/0896-6273(92)90171-9]
- Contet, C., Kieffer, B. L., & Befort, K. (2004). Mu opioid receptor: A gateway to drug addiction. Current Opinion in Neurobiology, 14(3), 370-8. [DOI:10.1016/j.conb.2004.05.005] [PMID]
- Destexhe, Z. F. M. A., & Sejnowski, T. J. (1998). Kinetic models of synaptic transmission. In C. Koch, & I. Segev (Eds.), Methods in Neuronal Modeling (pp. 1-25). Cambridge: MIT Press.
- Dong, Y., & Nestler, E. J. (2014). The neural rejuvenation hypothesis of cocaine addiction. Trends in Pharmacological Sciences, 35(8), 374-83. [DOI:10.1016/j.tips.2014.05.005] [PMID] [PMCID]
- Ga, B. (1980). Excitatory action of opioid peptides and opiates on cultured hippocampal pyramidal cells. Brain Research, 194(1), 193-203. [DOI:10.1016/0006-8993(80)91328-1]
- Harris, G., Wimmer, M., Byrne, R., & Aston-Jones, G. (2004). Glutamate-associated plasticity in the ventral tegmental area is necessary for conditioning environmental stimuli with morphine. Neuroscience, 129(3), 841-7. [DOI:10.1016/j.neuroscience.2004.09.018] [PMID]
- Heidari, M. H., Amini, A., Bahrami, Z., Shahriari, A., Movafag, A., & Heidari, R. (2013). Effect of chronic morphine consumption on synaptic plasticity of rat’s hippocampus: A transmission electron microscopy study. Neurology Research International, 2013, 290414. [DOI:10.1155/2013/290414] [PMID] [PMCID]
- Herman, B. H., Frankenheim, J., Litten, R. Z., Sheridan, P. H., Weight, F. F., & Zukin, S. R. (2003). Glutamate and addiction. New York: Humana Press.
- Hosseinmardi, N., Azimi, L., Fathollahi, Y., Javan, M., & Naghdi, N. (2011). In vivo sodium salicylate causes tolerance to acute morphine exposure and alters the ability of high frequency stimulation to induce long-term potentiation in hippocampus area CA1. European Journal of Pharmacology, 670(2), 487-94. [DOI:10.1016/j.ejphar.2011.09.008] [PMID]
- Hosseinmardi, N., Fathollahi, Y., Naghdi, N., & Javan, M. (2009). Theta pulse stimulation: a natural stimulus pattern can trigger long-term depression but fails to reverse long-term potentiation in morphine withdrawn hippocampus area CA1. Brain Research, 1296, 1-14. [DOI:10.1016/j.brainres.2009.08.020] [PMID]
- Kauer, J. A., & Malenka, R. C. (2007). Synaptic plasticity and addiction. Nature Reviews Neuroscience, 8(11), 844-58. [DOI:10.1038/nrn2234] [PMID]
- Kelley, A. E. (2004). Memory and addiction: Shared neural circuitry and molecular mechanisms. Neuron, 44(1), 161-79. [DOI:10.1016/j.neuron.2004.09.016] [PMID]
- Kow, L. M., Commons, K., Ogawa, S., & Pfaff, D. (2002). Potentiation of the excitatory action of NMDA in ventrolateral periaqueductal gray by the μ-opioid receptor agonist, DAMGO. Brain Research, 935(1), 87-102. [DOI:10.1016/S0006-8993(02)02532-5]
- Li, J., Tang, J., Ma, J., Du, M., Wang, R., & Wu, Y. (2016). Dynamic transition of neuronal firing induced by abnormal astrocytic glutamate oscillation. Scientific Reports, 6(1), 32343. [DOI:10.1038/srep32343]
- Lisman, J., Yasuda, R., & Raghavachari, S. (2012). Mechanisms of CaMKII action in long-term potentiation. Nature Reviews Neuroscience, 13(3), 169-82. [DOI:10.1038/nrn3192] [PMID] [PMCID]
- Lüscher, C., & Malenka, R. C. (2011). Drug-evoked synaptic plasticity in addiction: From molecular changes to circuit remodeling. Neuron, 69(4), 650-63. [DOI:10.1016/j.neuron.2011.01.017] [PMID] [PMCID]
- Mameli, M., Bellone, C., Brown, M. T., & Lüscher, C. (2011). Cocaine inverts rules for synaptic plasticity of glutamate transmission in the ventral tegmental area. Nature Neuroscience, 14(4), 414-6. [DOI:10.1038/nn.2763] [PMID]
- Mao, J. (1999). NMDA and opioid receptors: their interactions in antinociception, tolerance and neuroplasticity. Brain Research Reviews, 30(3), 289-304. [DOI:10.1016/S0165-0173(99)00020-X]
- Mishra, P. R., Barik, M., & Ray, S. B. (2017). Effect of nimodipine on morphine-related withdrawal syndrome in rat model: An observational study. Journal of Pediatric Neurosciences, 12(1), 7. [DOI:10.4103/1817-1745.205652] [PMID] [PMCID]
- Moradi, K., Moradi, K., Ganjkhani, M., Hajihasani, M., Gharibzadeh, S., & Kaka, G. (2013). A fast model of voltage-dependent NMDA receptors. Journal of Computational Neuroscience, 34(3), 521-31. [DOI:10.1007/s10827-012-0434-4] [PMID]
- Nestler, E. J. (2001). Molecular basis of long-term plasticity underlying addiction. Nature Reviews Neuroscience, 2(2), 119-28. [DOI:10.1038/35053570] [PMID]
- Nestler, E. J. (2013). Cellular basis of memory for addiction. Dialogues in Clinical Neuroscience, 15(4), 431. [PMID] [PMCID]
- Peters, J., & De Vries, T. J. (2012). Glutamate mechanisms underlying opiate memories. Cold Spring Harbor Perspectives in Medicine, 2(9), a012088. [DOI:10.1101/cshperspect.a012088] [PMID] [PMCID]
- Przewlocki, R., Parsons, K. L., Sweeney, D. D., Trotter, C., Netzeband, J. G., Siggins, G. R., et al. (1999). Opioid enhancement of calcium oscillations and burst events involving NMDA receptors and L-type calcium channels in cultured hippocampal neurons. The Journal of Neuroscience, 19(22), 9705-15. [DOI:10.1523/JNEUROSCI.19-22-09705.1999] [PMID]
- Rezai, X., Kieffer, B. L., Roux, M. J., & Massotte, D. (2013). Delta opioid receptors regulate temporoammonic-activated feedforward inhibition to the mouse CA1 hippocampus. PloS One, 8(11), e79081. [DOI:10.1371/journal.pone.0079081] [PMID] [PMCID]
- Sanhueza, M., & Lisman, J. (2013). The CaMKII/NMDAR complex as a molecular memory. Molecular Brain, 6(1), 10. [DOI:10.1186/1756-6606-6-10] [PMID] [PMCID]
- Tewari, S., & Majumdar, K. (2012a). A mathematical model for astrocytes mediated LTP at single hippocampal synapses. Journal of Computational Neuroscience, 33(2), 341-70. [DOI:10.1007/s10827-012-0389-5] [PMID]
- Tewari, S. G., & Majumdar, K. K. (2012b). A mathematical model of the tripartite synapse: Astrocyte-induced synaptic plasticity. Journal of Biological Physics, 38(3), 465-96. [DOI:10.1007/s10867-012-9267-7] [PMID] [PMCID]
- Trujillo, K. A. (2002). The neurobiology of opiate tolerance, dependence and sensitization: Mechanisms of NMDA receptor-dependent synaptic plasticity. Neurotoxicity Research, 4(4), 373-91. [DOI:10.1080/10298420290023954] [PMID]
- Tsodyks, M. V., & Markram, H. (1997). The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability. Proceedings of the national academy of sciences, 94(2), 719-23. [DOI:10.1073/pnas.94.2.719]
- van Huijstee, A. N., & Mansvelder, H. D. (2015). Glutamatergic synaptic plasticity in the mesocorticolimbic system in addiction. Frontiers in Cellular Neuroscience, 8, 466. [DOI:10.3389/fncel.2014.00466]
- Volman, V., Bazhenov, M., & Sejnowski, T. J. (2012). Computational models of neuron-astrocyte interaction in epilepsy. Frontiers in Computational Neuroscience, 6, 58. [DOI:10.3389/fncom.2012.00058] [PMID] [PMCID]
- Williams, J. T., Christie, M. J., & Manzoni, O. (2001). Cellular and synaptic adaptations mediating opioid dependence. Physiological Reviews, 81(1), 299-343. [DOI:10.1152/physrev.2001.81.1.299] [PMID]
- Wolf, M. E. (2003). LTP may trigger addiction. Molecular Interventions, 3(5), 248. [DOI:10.1124/mi.3.5.248] [PMID]
- Zhabotinsky, A. M. (2000). Bistability in the Calmodulin-dependent protein kinase-phosphatase system. Biophysical Journal, 79(5), 2211-21. [DOI:10.1016/S0006-3495(00)76469-1]

Type of Study: Original |
Subject:
Computational Neuroscience
Received: 2017/06/7 | Accepted: 2017/10/4 | Published: 2018/07/1
Received: 2017/06/7 | Accepted: 2017/10/4 | Published: 2018/07/1
Send email to the article author
| Rights and permissions | |
 |
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License. |












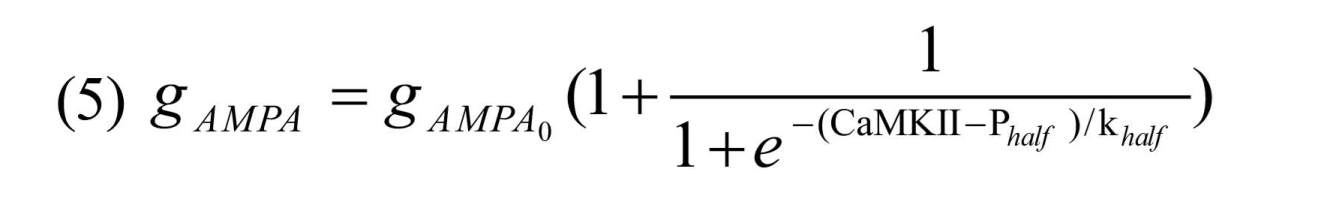
.jpg)